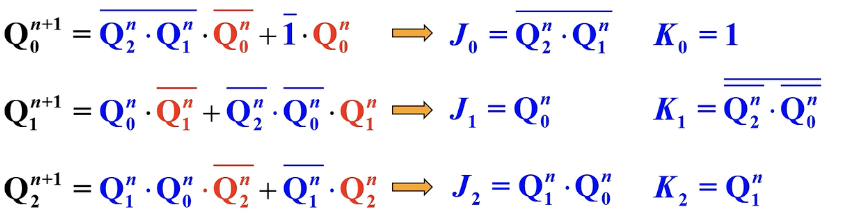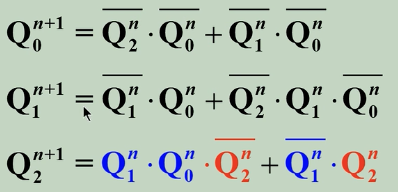数字逻辑电路笔记
数字逻辑电路笔记📒
✨目录
[TOC]
作者的废话:关于数字逻辑电路笔记,我决定全部塞在一片文章。✍️
阅读本文注意事项:
❌错误查看方式:直接在Gitee上阅读
🙆正确查看方式:复制到Typora或者其他支持Markdown查看/编辑软件上阅读,如:VisualStudio、SublimeText等
半加器
输入:两个1位的二进制数
输出:进位+本位
特点:不考虑低位的进位。
规定符号:
- 本位和 -
S - 半加进位 -
C
因为是1位,所以输入只有1或0两种可能。那么总共就只有三种可能性:0+0=0,0+1=1,1+1=2,其中1+1=2产生了进位,本位就是0进位是1。
可以列出真值表(A、B为输入,S、C为输出):
| A | B | S | C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
也可以写出逻辑表达式:
对应的逻辑图:
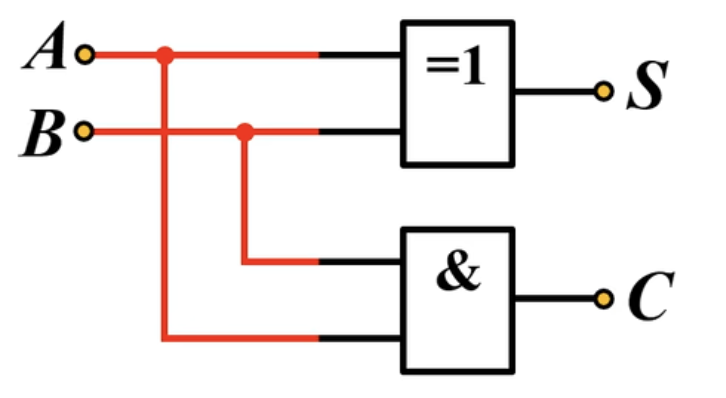
平常主要是用的是半加器的逻辑符号:
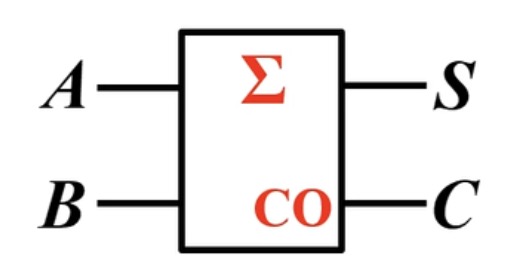
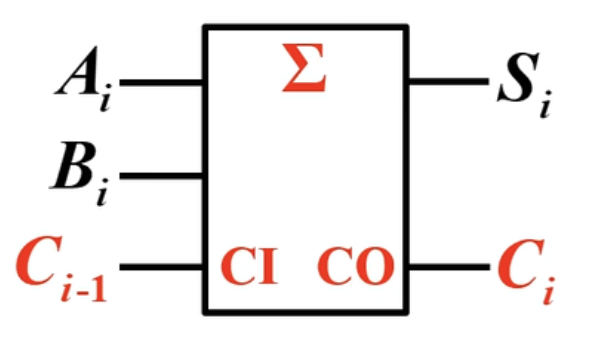
全加器
全加器与半加器唯一的区别就是考虑了低位的进位,所以输入也增加了一个:低位的进位。
规定的符号:
低位的进位:
向高位的进位:
本位:
对应的真值表如下:
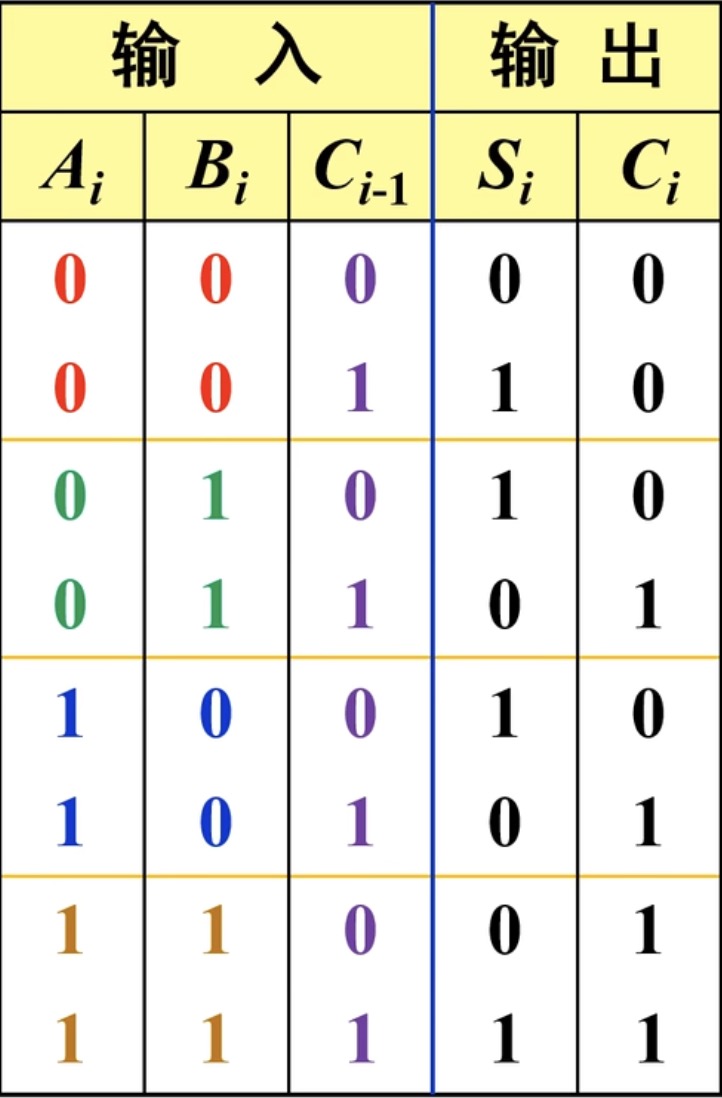
逻辑表达式:
全加器对应的逻辑符号:
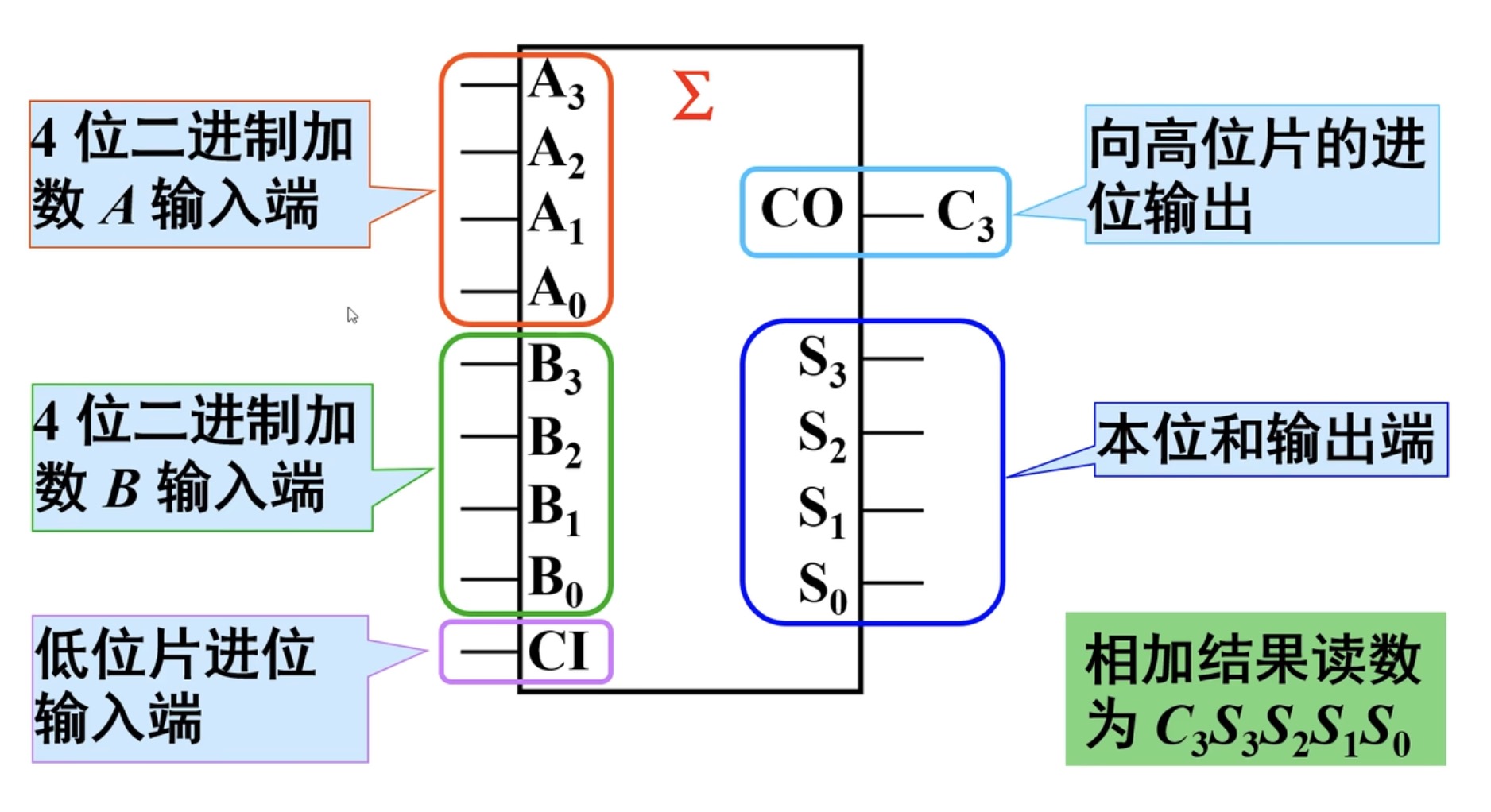
集成全加器
集成全加器有两种,TTL的全加器和CMOS的C661全加器
- TTl:74LS183
- CMOS:C661
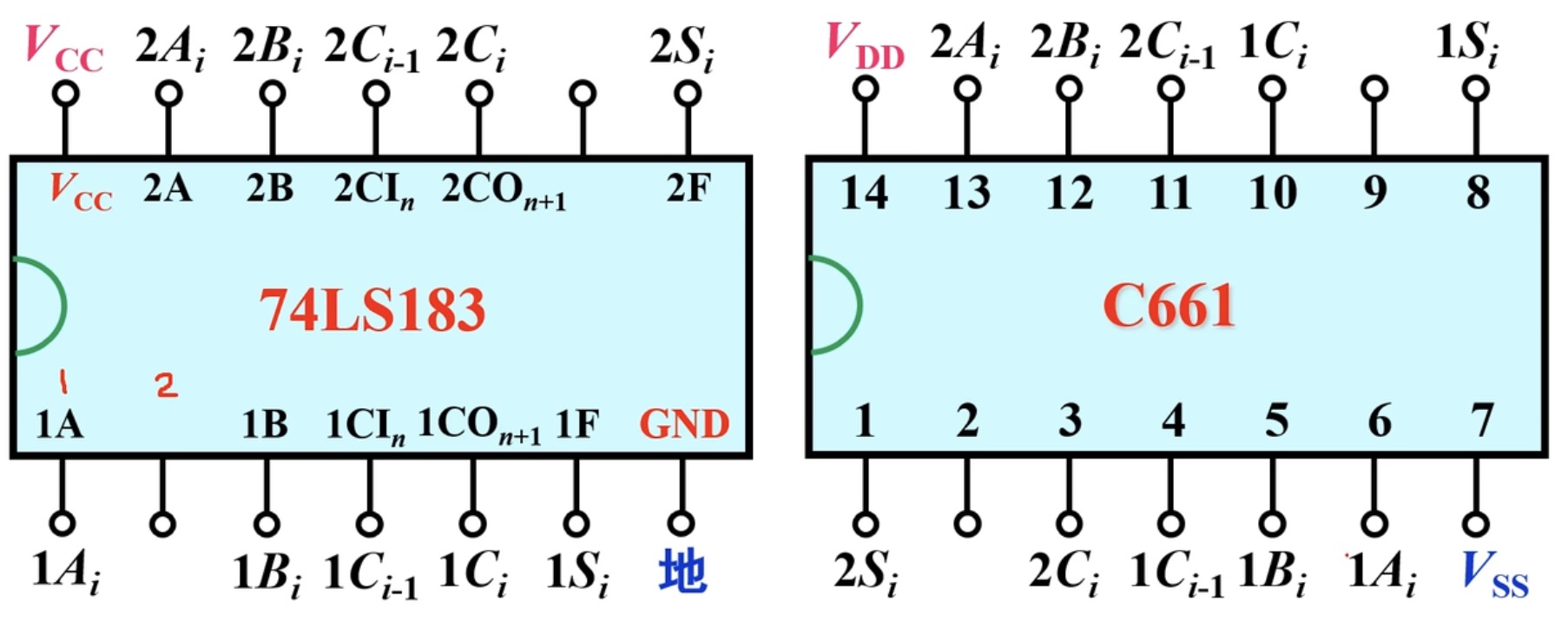
需要说明的是,这里的两个集成全加器各自都有两个管角是空的,这代表这几个管角没有任何功能,不用管它。
至于原因,是为了匹配插座特意设计出来的,常用的管角数量为14、16,偏偏就是没有12管角的,所以如果设计成12个管角,很可能找不到对应的插座,于是便多出来了两个管角。
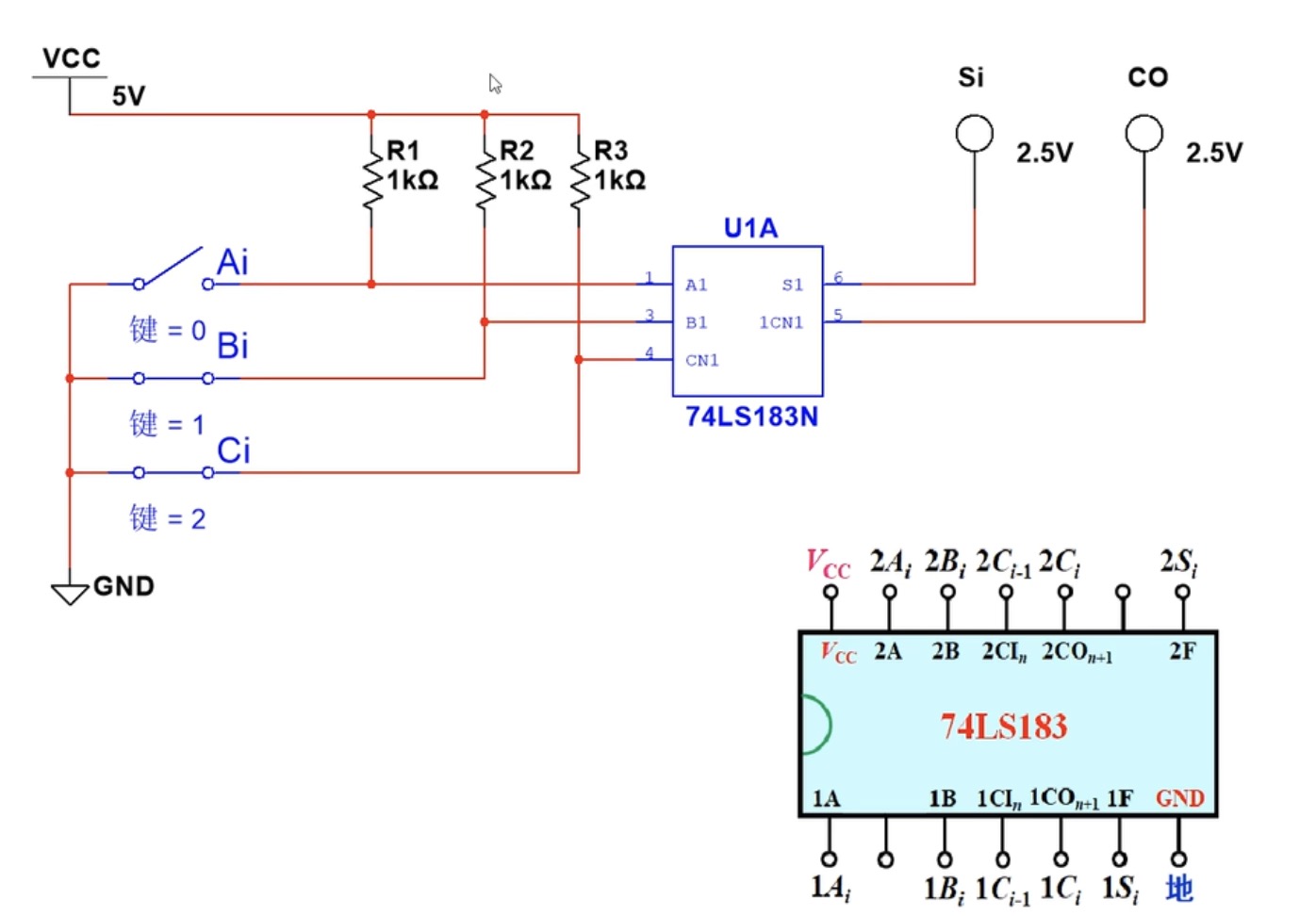
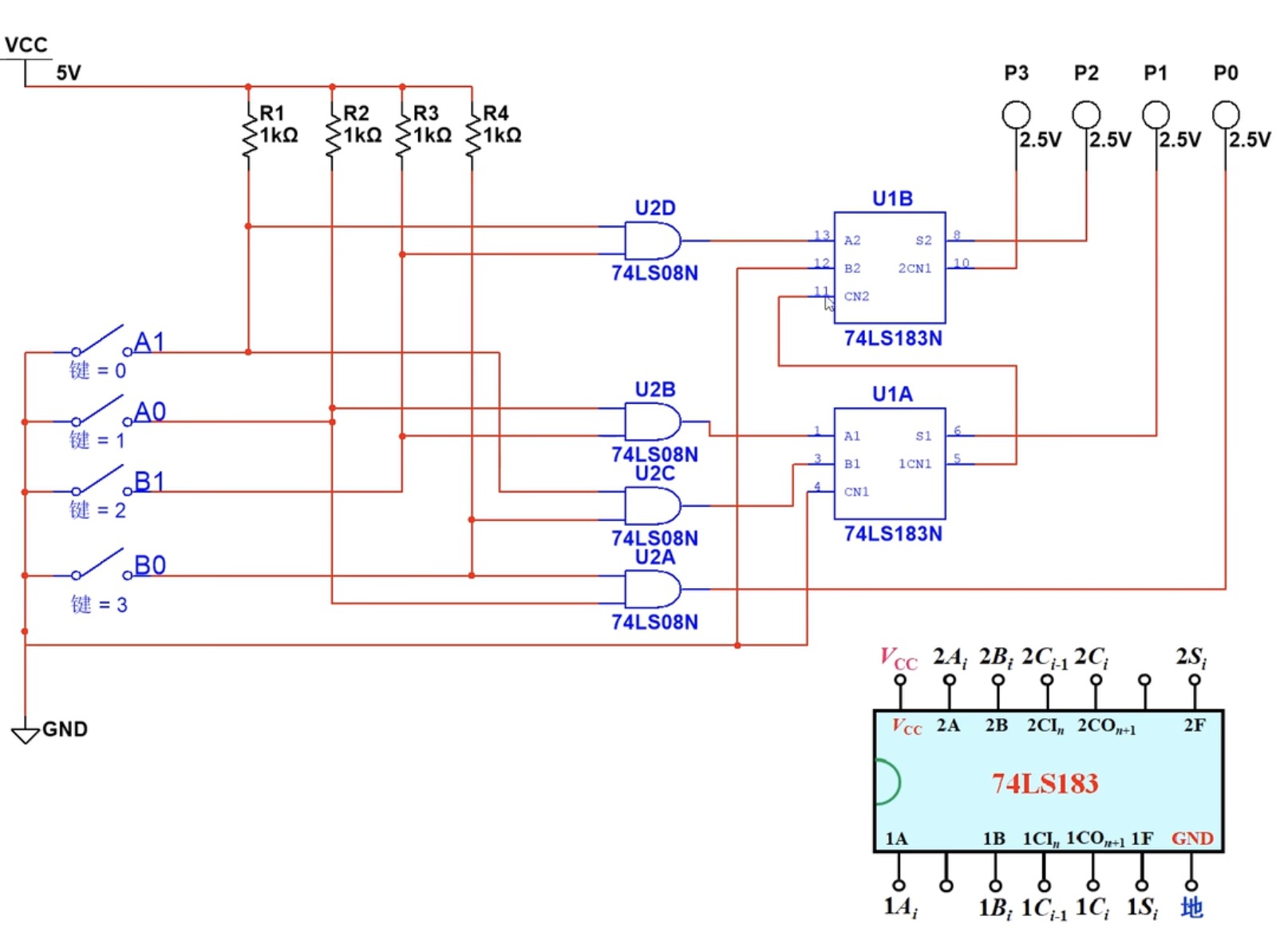
集成全加器的仿真:
可以在Multism中搭建如图所示的电路来仿真全加器,在你拖拽出74LS183集成电路的时候,你会发现系统会让你选择A|B,这里的A和B就是74LS183上的两个全加器,你可以选择其中的一个进行放置。
乘法器
二进制的所有运算皆基于二进制的加法器,以两位二进制相加为例。
形式如:
01*11、11*11这种。
所以就可以写出表达式(这里的
我们假设,
那么
类比十进制中两位数的加法可以写出这样的式子:
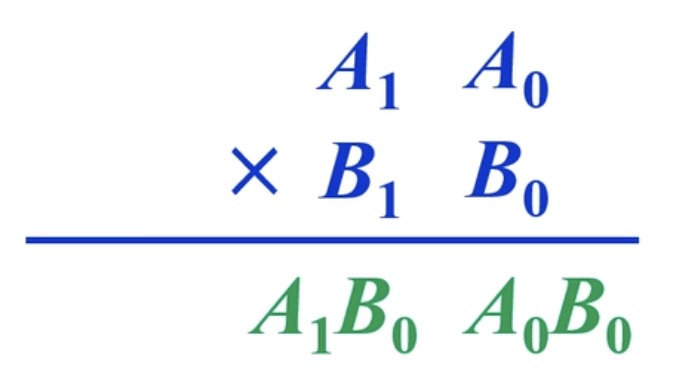
因为
通过这样的式字,我们可以发现两位二进制的乘法就被转化成了加法和与运算,也就是说使用全加器和与门就可以实现一个乘法器☝️🤓。
这样我们就可以写出对应的逻辑电路图(只用到了与门和加法器)。
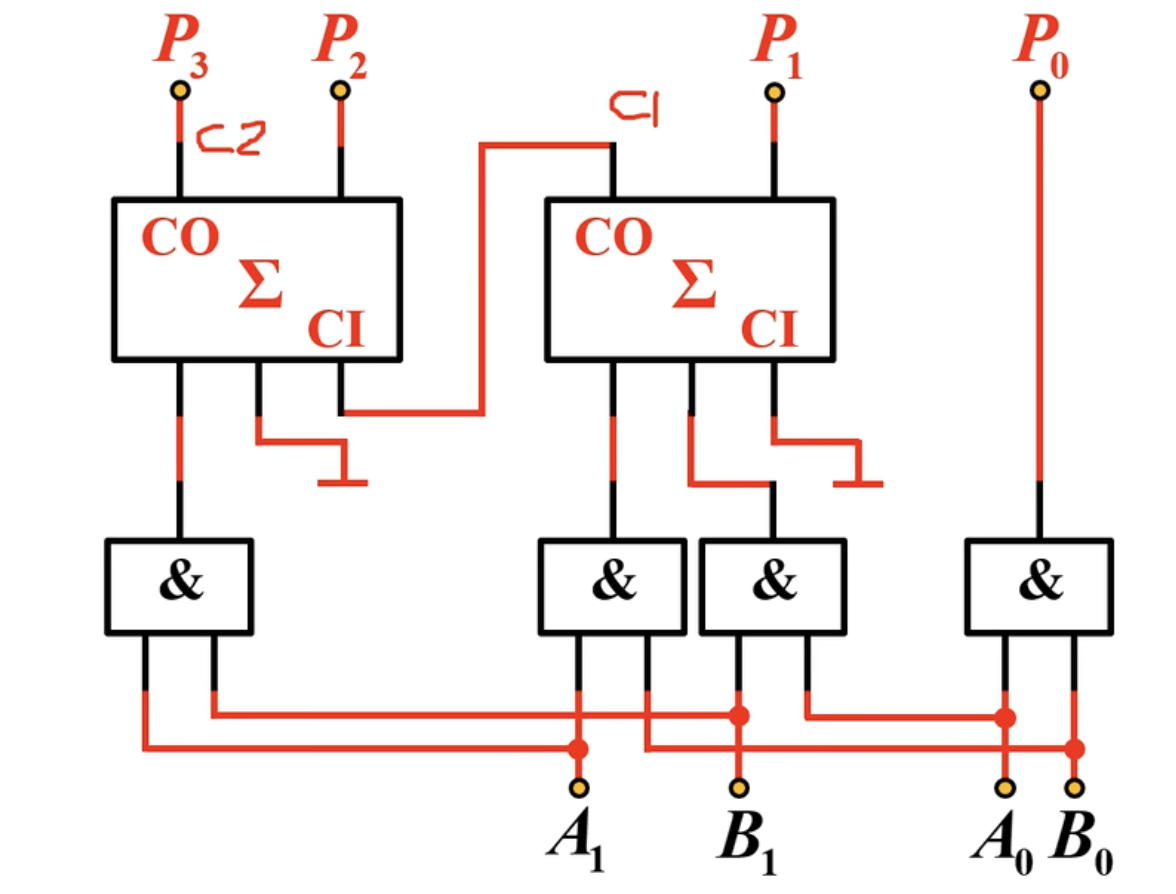
可以在Multism中设计仿真电路图:
多位二进制的加法器
前面说到的加法器都仅限于一位的二进制之间的加法,然而对于多位二进制的加法有两种。
- 串行进位加法器
- 超前进位加法器(并行进位加法器)
- 串行进位加法器:
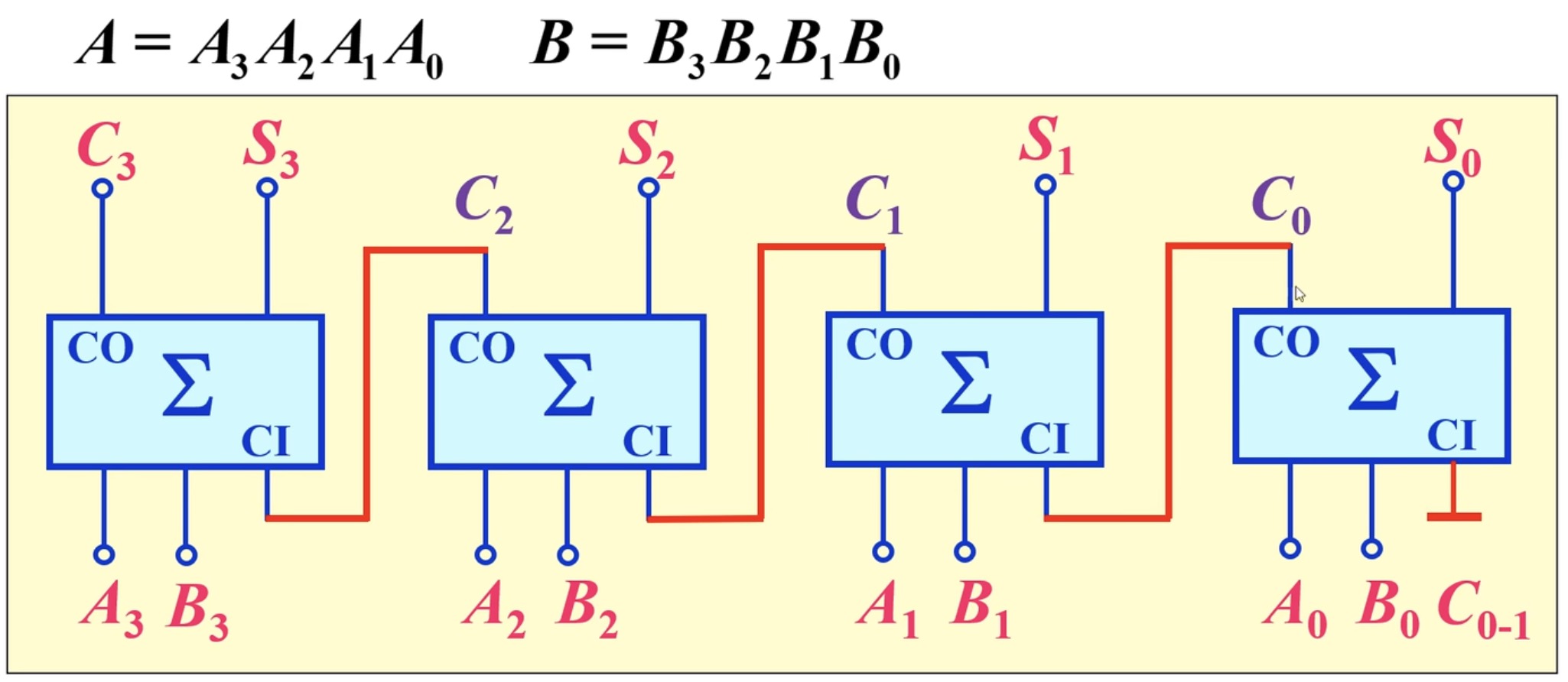
可以看出这种加法器就是把全加器串在了一起,每个全加器都要等待上一个全加器的高位进位输出作为自己的输入,所以会导致一个结果☝️:不能做到同时执行加法器,运行速度缓慢。
总结一下串行进位加法器的特点:
- 电路简单,容易连接
- 速度低
- 并行进位加法器
同样的,有下面的特点:
- 内部电路复杂
- 运行速度快(同时执行)
编码器的概念
编码的概念:将二进制转成十进制称之为解码,将十进制转换成二进制称之为编码。
编码器:将十进制转换成二进制的电路称之为编码器,简单来说就是将我们熟悉的十进制编译成计算机认识的二进制代码,所以叫做编码。
编码器的分类:
- 二进制编码器
- 二-十进制编码器
- 优先编码器
我们知道,一位二进制可以表示两种信息,两位二进制可以表示四种信息,三位则可以表示八种信息。也就是说,
也就是,
- 全编码 - 部分编码
二进制编码器
例如:设计一个能将
设计如下真值表:
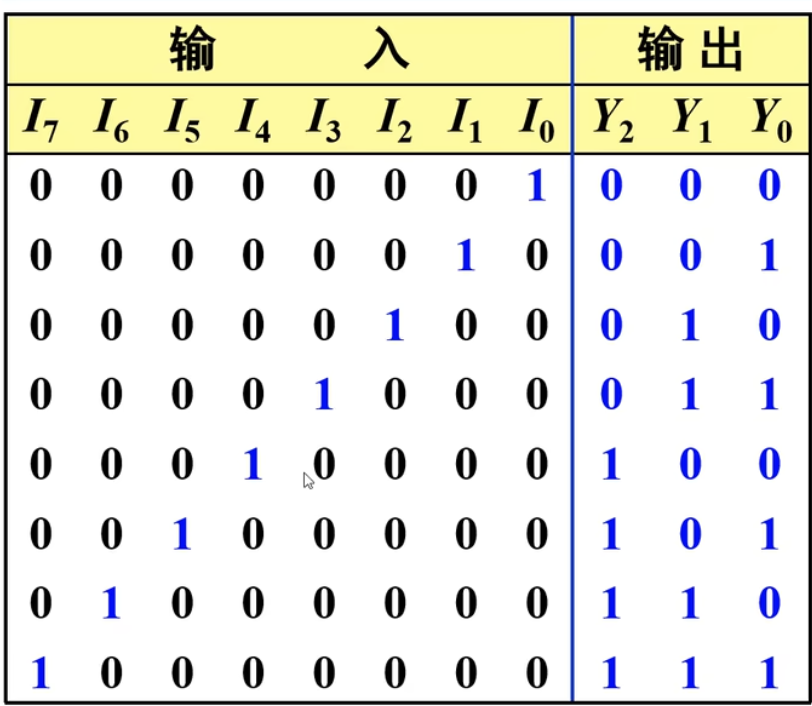
然后写出对应的表达式:
例:

得到逻辑图:
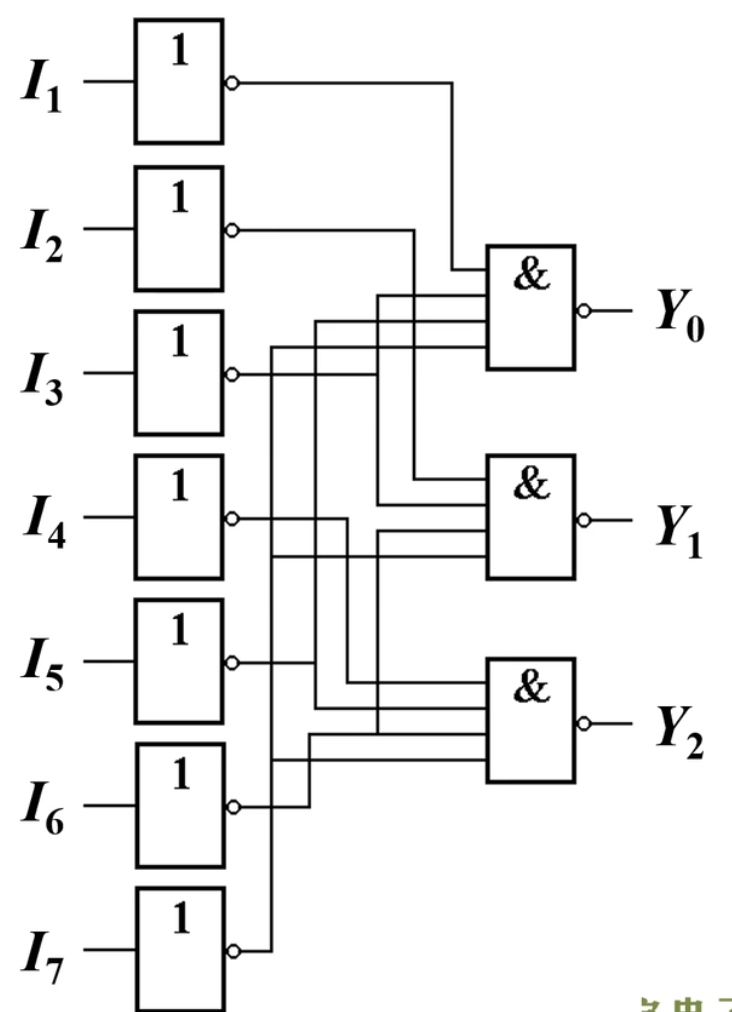
这里
优先编码器
功能:输入多个十进制数,根据优先级高低,优先取优先级最高的数字其余不看。
例如:给定优先级规则为数字越大优先级越高,那么输入多个十进制优先取数字大的作为输入,其余不看,也就是输入8、7、3这三个数,直接取8作为输入其余不看。所以下方的真值表中有八叉X,代表输入什么都无所谓,因为比他大的树字会被优先取。
真值表:
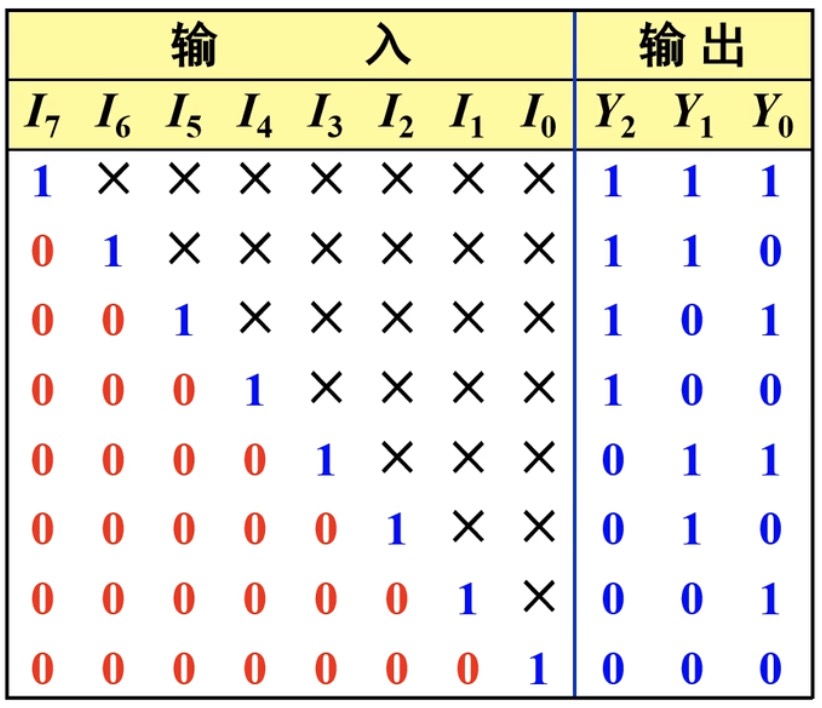
可以写出对应的逻辑表达式:
注意这里也是根据
规则来华化简后的结果。
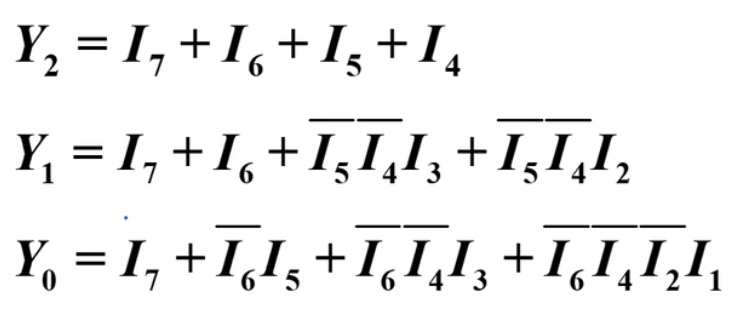
8线 - 3线优先编码器 74LS48:
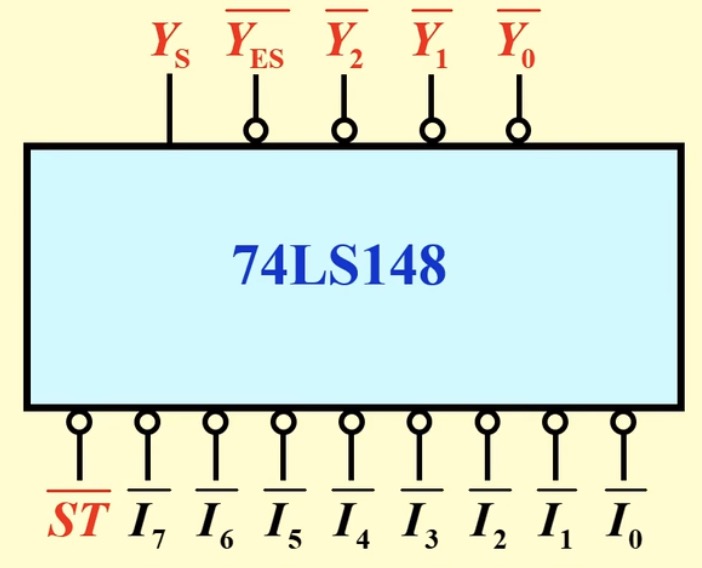
、 、
这里加了非号,表示将所有输入和输出取非,也就是说输入从之前的1有效变成了 0 才有效。
对应的真值表:
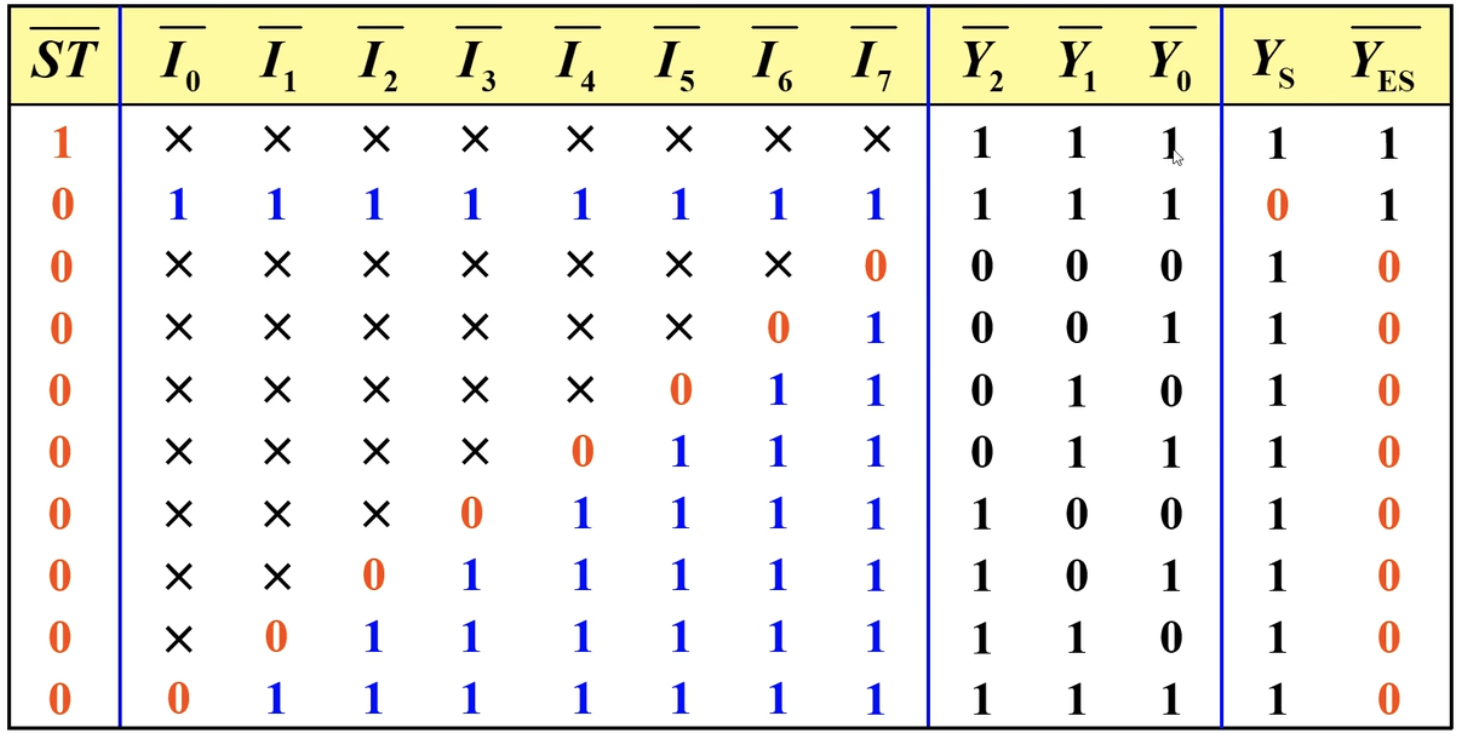
这里的
- 在上面所有的输入中,
Multism仿真电路设计:
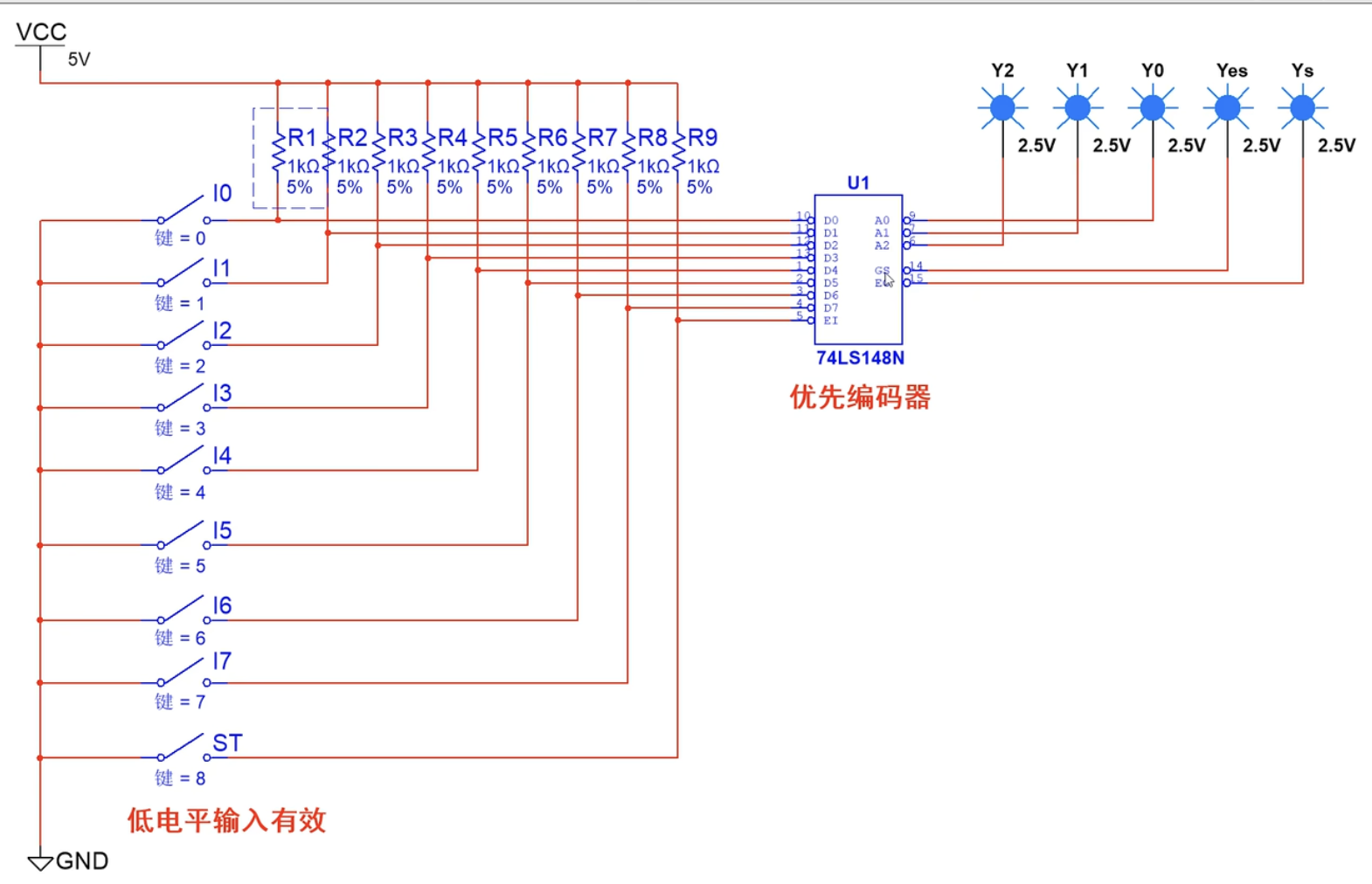
与非门RS触发器
一、电路组成:
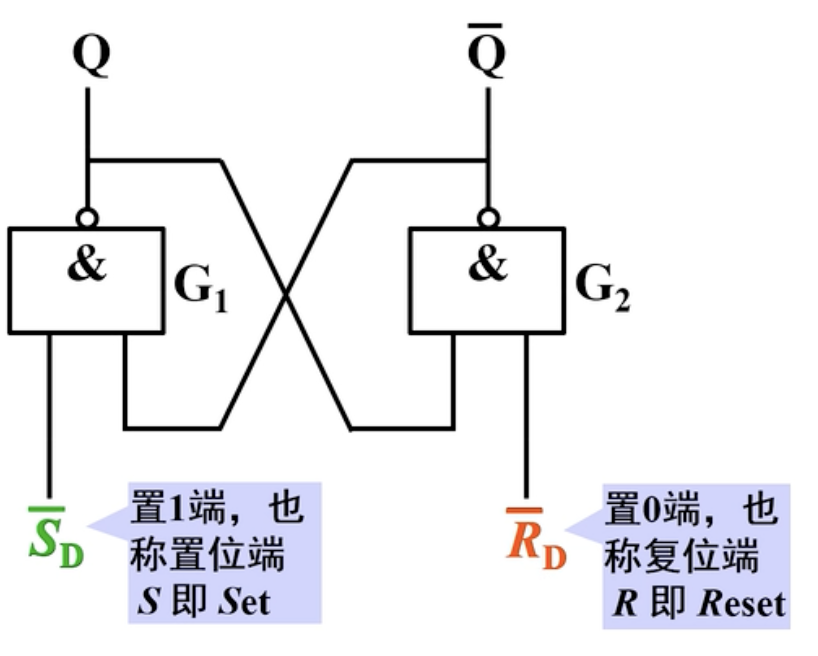
这里的
只要看到输入输出为取非的符号,就需要知道这里是低电平有效。
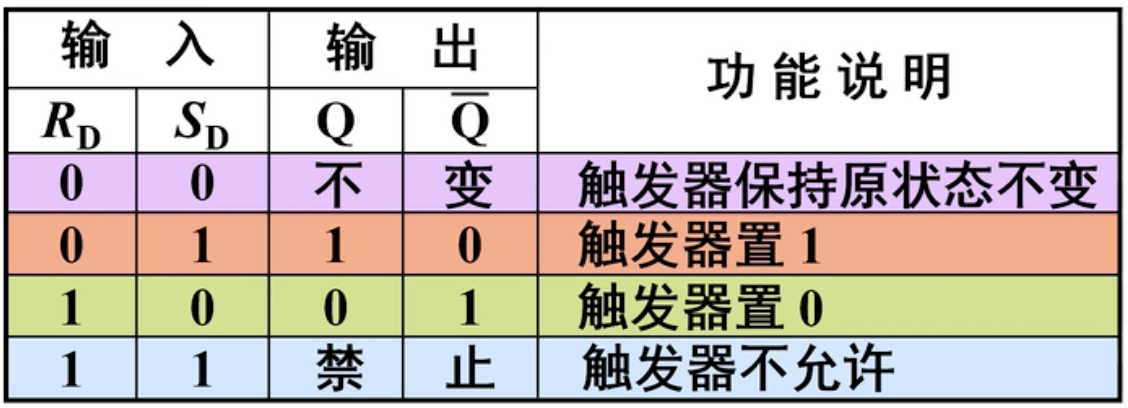
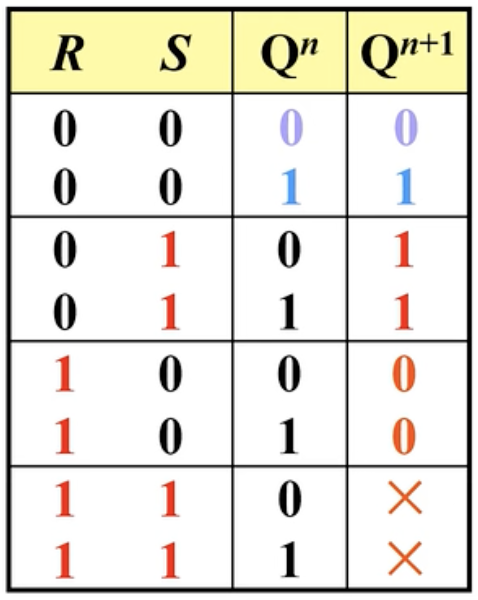
二、逻辑功能(不考虑现态和次态)
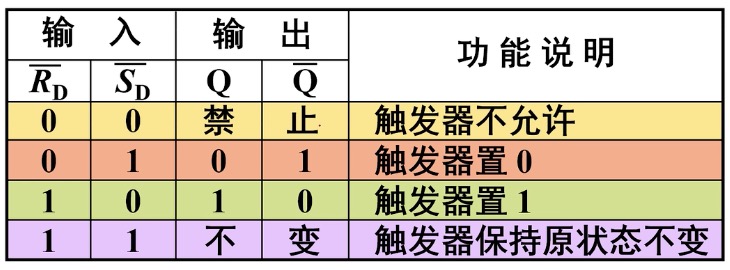
这张图告诉我们,Set有效(置0)的时候,将Q设置为有效(置1);Reset有效时将Q设置为无效。当Set和Reset都无效就相当于输入没有更新状态不做改变,当Reset和Set都有效是一种不合理的情况,需要避免并且在逻辑上是不被允许的。
对于RS触发器,不需要死记真值表,理解Reset和Set的概念就算学会了。
三、特性表
在上述RS触发器的基础上增加了下一次的状态
- 现态
- 次态
现态和次态是两个相邻时间里触发器输出端的状态。
真值表:
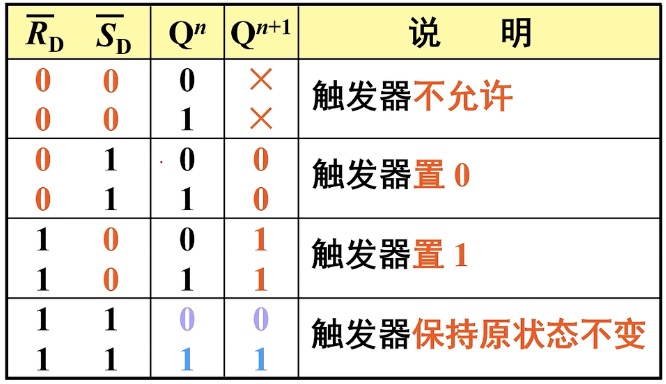
注意⚠️:低电平(置零)有效。
约束条件:
四、特性方程
由于上面这张真值表有重复信息(
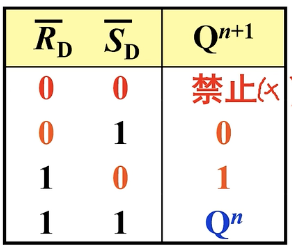
用卡诺图表示出来:
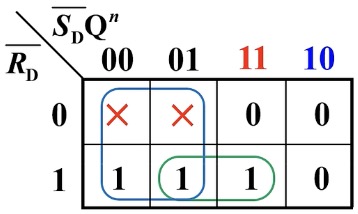
得到特性方程:
- 约束条件:
五、状态转换图
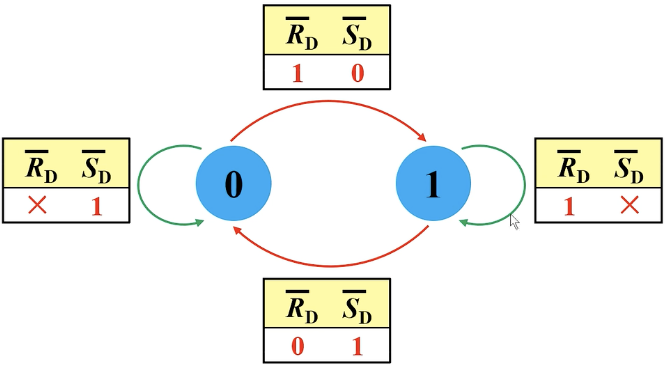
X表示0或者1两种情况。
六、驱动表
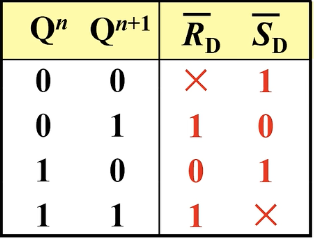
根据输出来判定输入的情况的真值表叫做驱动表。
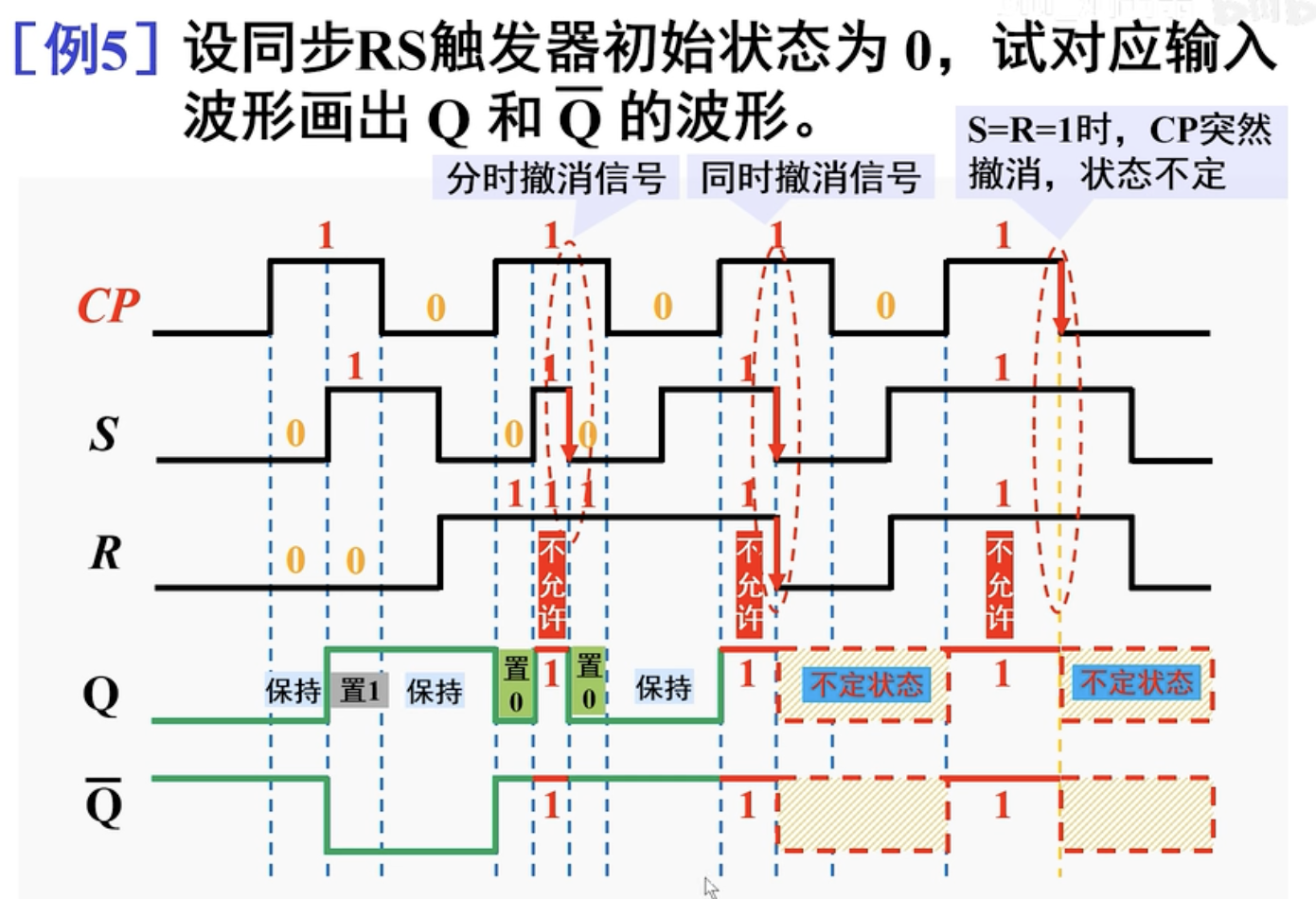
[例1]:设触发器初始状态为0,试对应输入波形画出
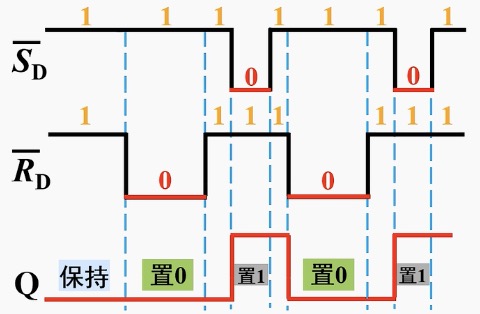
这里
省略,将 取反即可。
[例2]:信号的分时撤销和同时撤销。
上面提到,当Reset和Set同时有效也就是违反约束条件的情况,这时需要将信号调整成正常的情况,那么就会出现信号的分时撤销和延时撤销。
我们知道0为有效电平,当
分时撤销:
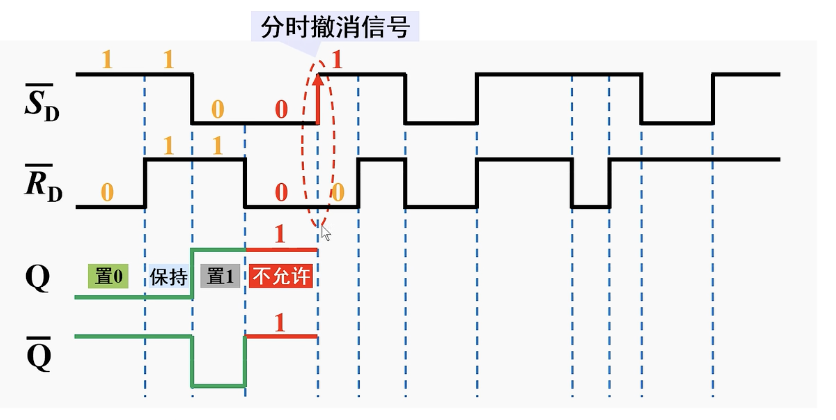
分时撤销取决于后撤销的信号,跟正常状态相同的分析。
例如,上图中
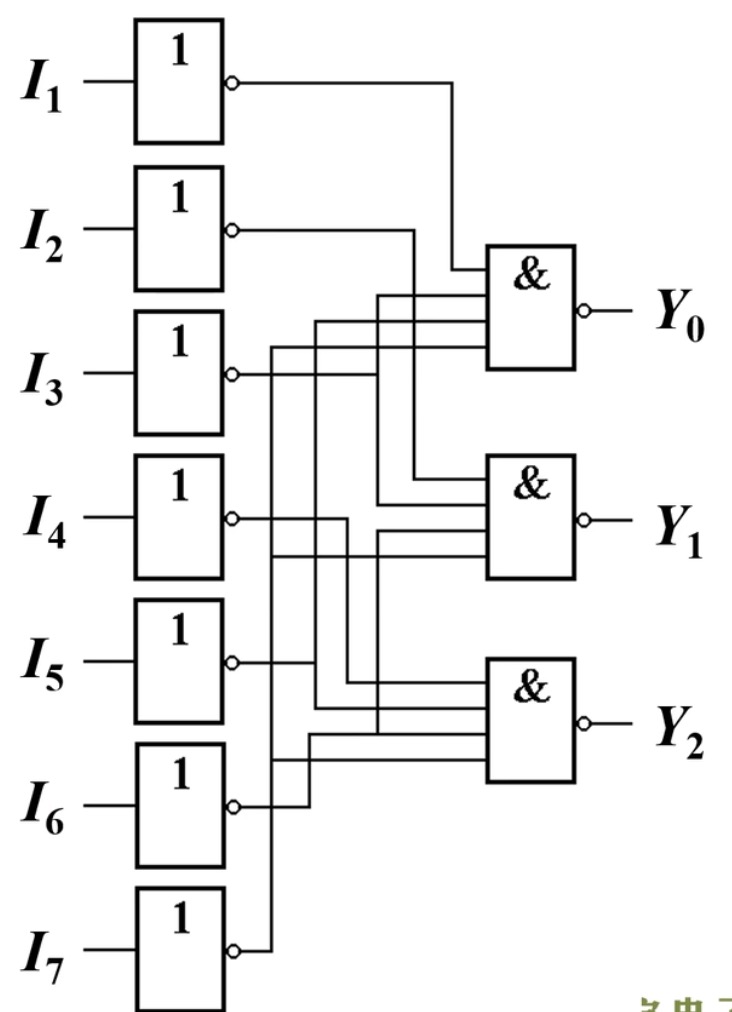
同时撤销:
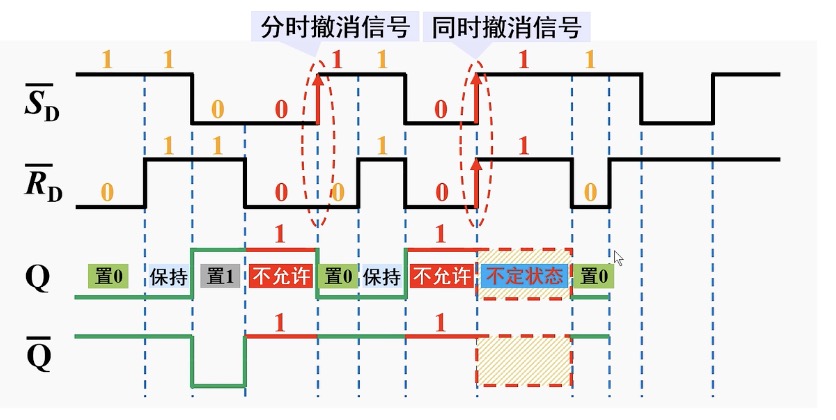
同时撤销根据电路内部的延时状态等复杂情况决定谁先起作用,状态不定(竞态)。
或非门RS触发器
一、电路组成:
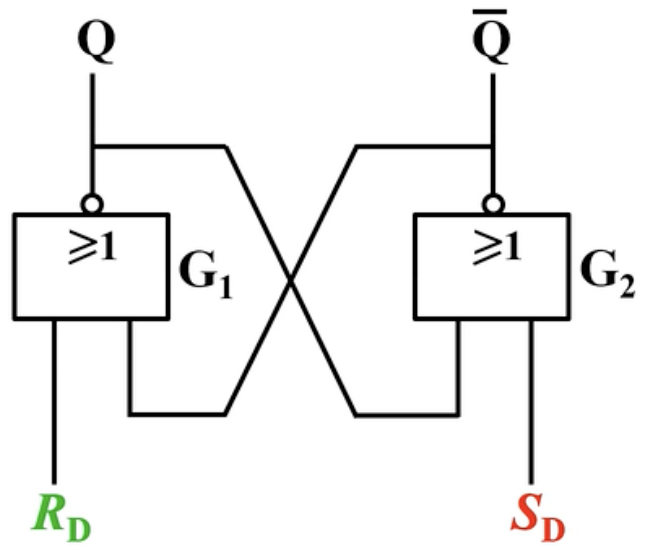
二、逻辑功能
三、特性表
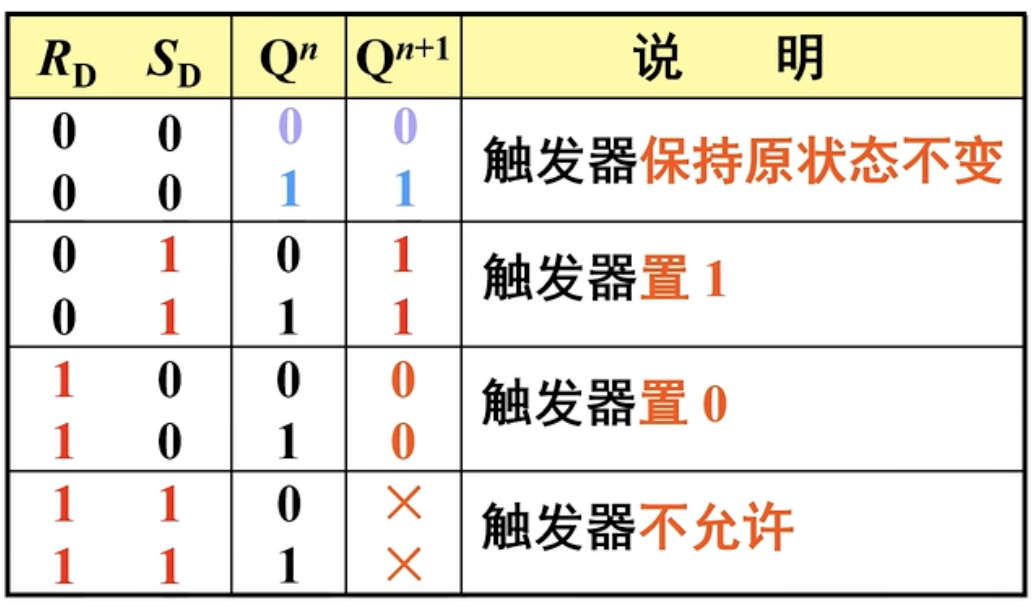
注意:与与非门RS触发器不同,高电平有效。
约束条件:
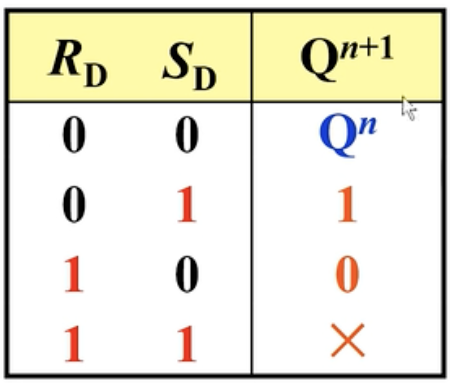
可以得到简化的特性表:
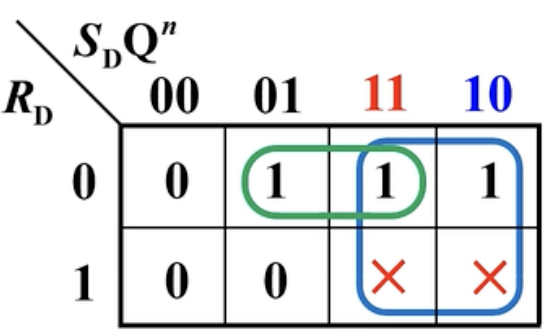
画出卡诺图如下:
得到最终的特性方程:
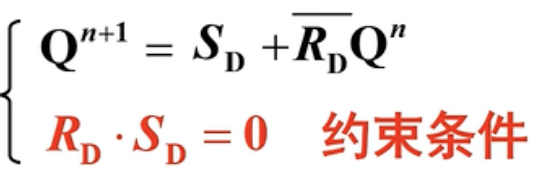
两种RS触发器的对比
逻辑符号对比:
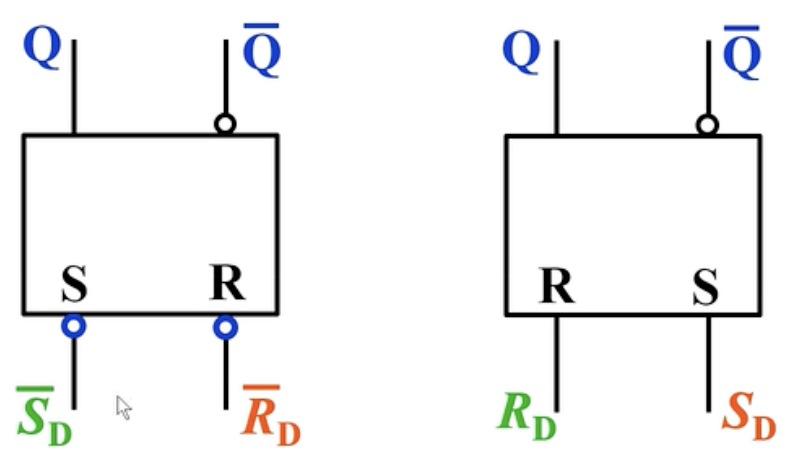
可以发现,
- 与非门RS触发器低电平有效,或非门RS触发器高电平有效。
- 与非门RS触发器左边为Set端口,右边为Reset端口;或非门RS触发器左边为Reset端口,右边为Set端口。
基本RS触发器的优缺点如下:
- 优点:电路简单,是构成各种触发器的基础🎉。
- 缺点:输入有约束条件;抗干扰能力差👎。
同步RS触发器
一、电路组成
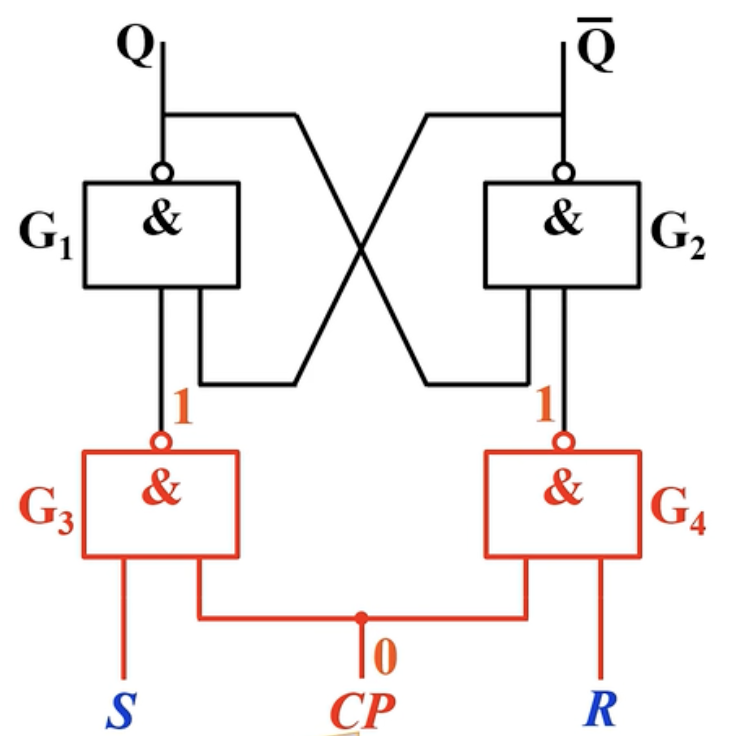
与原来的与非门RS触发器相比增加了两个与非门,由时钟CP控制的门
二、逻辑功能
特性表如图所示:
高电平为有效信号📶。
对应的逻辑符号:
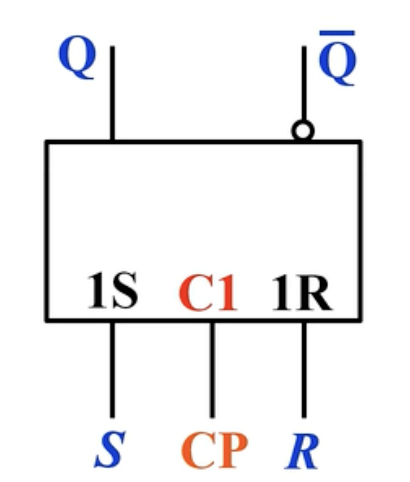
包含异步端的同步RS触发器的逻辑符号如下:
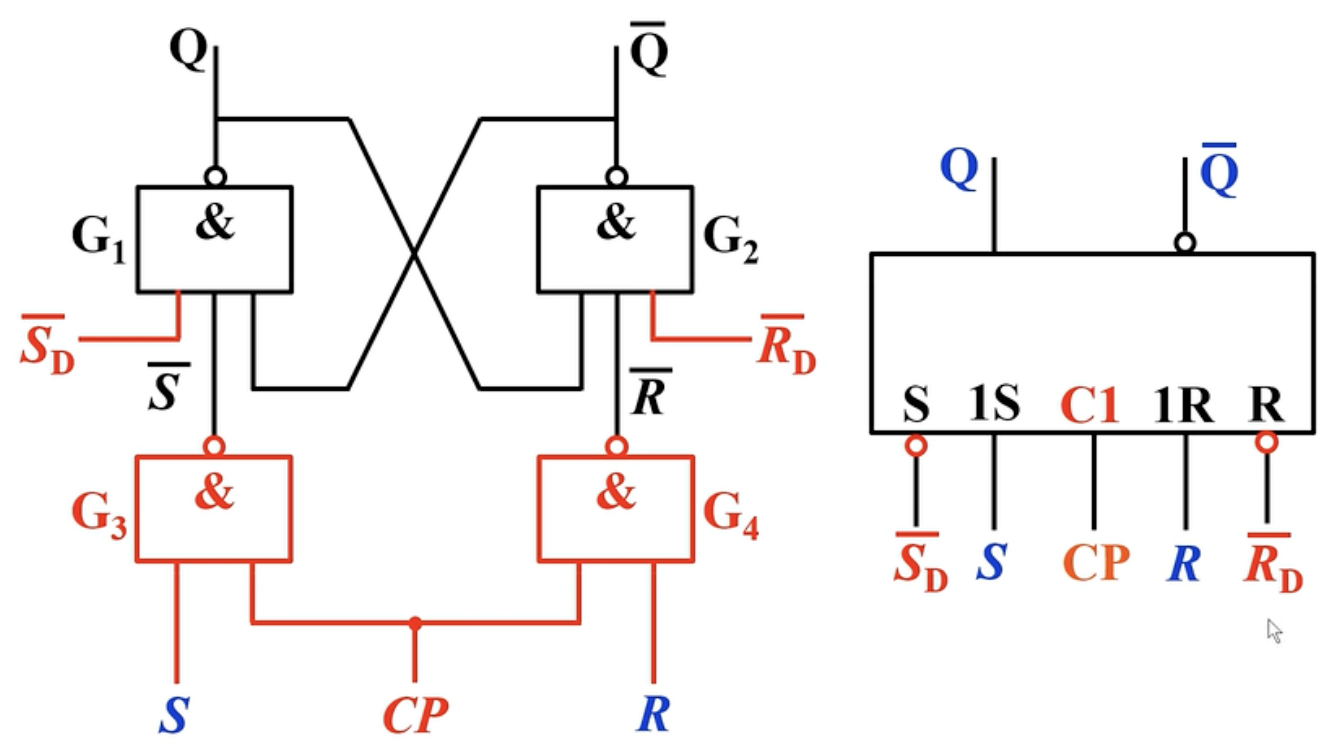
、 、 、 、
可以起到预置触发器初始状态的作用,平时不工作时需要将 、 置为 、 。其实所谓的同步输入端与异步输入端就是看受不受到 端的控制,收到控制就得等到一起作用,不受到控制就异步了。
三、特性表 => 特性方程
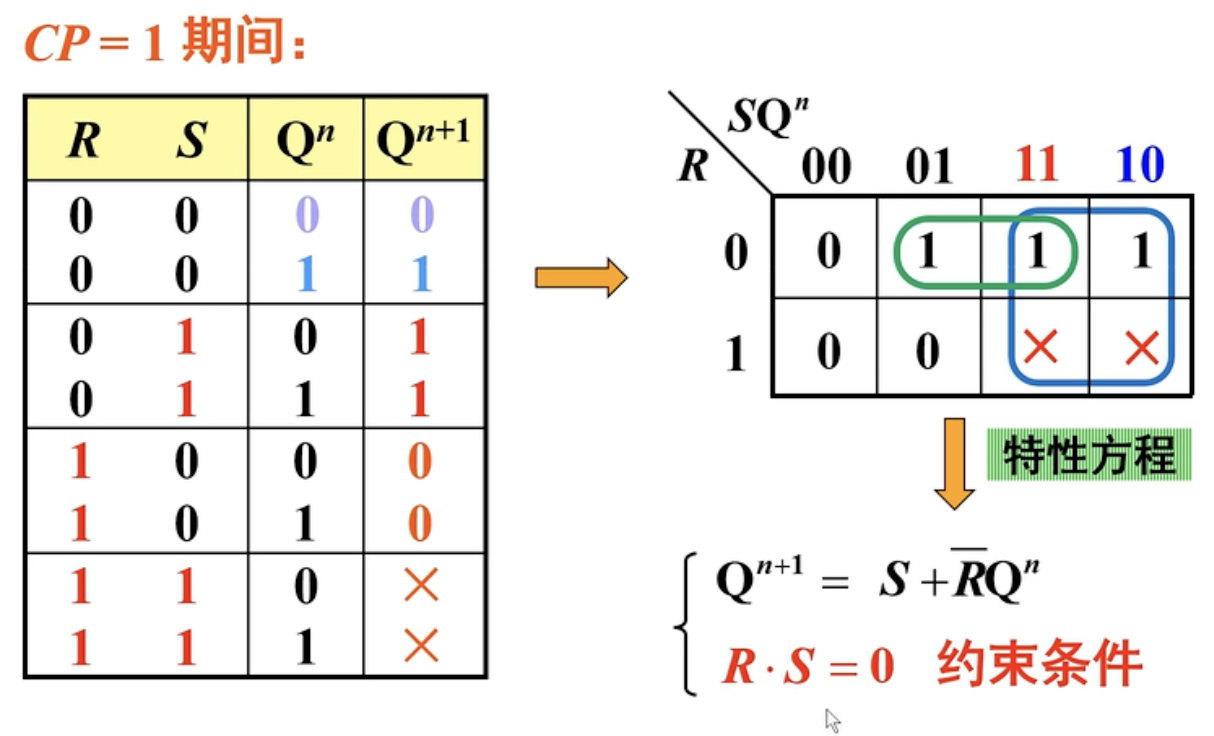
这个特性方程有效的前提一定是
等于 。
四、状态转换图
容易得到对应的状态转换图:
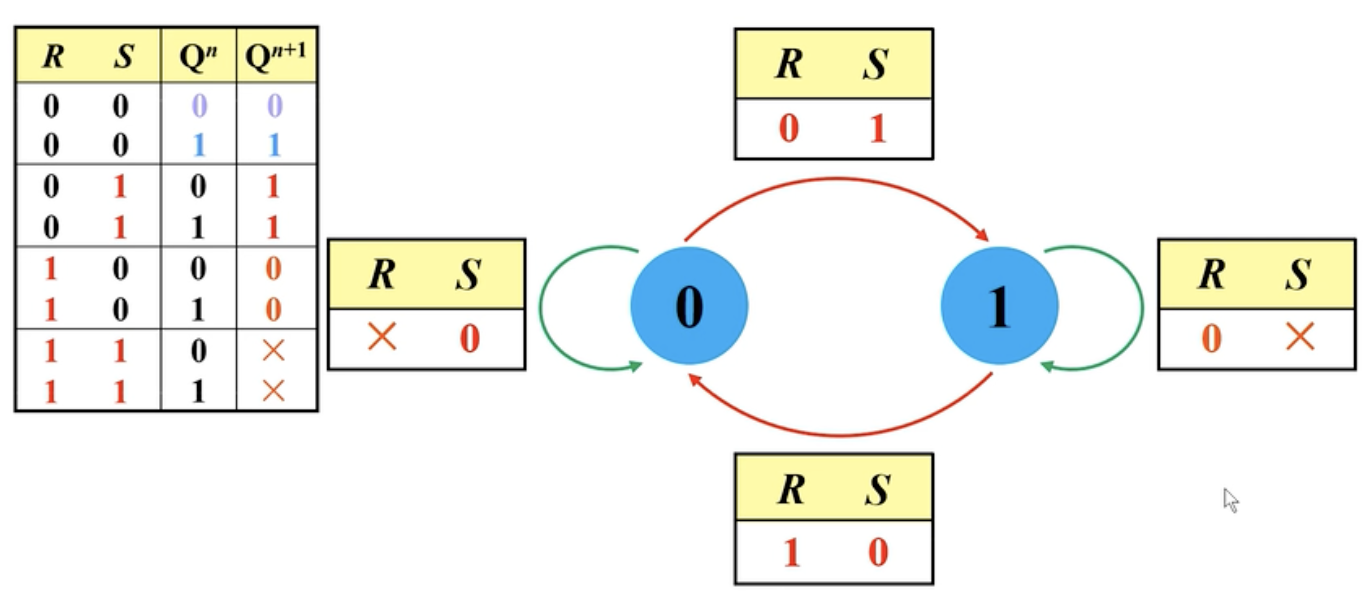
五、同步RS触发器的优缺点
- 优点:有了
- 缺点:仍然存在不定状态,
、
一个需要注意的细节⚠️:如果
为 、 这时是处于无效状态,如果这个时候 从 变成 但是 保持不变就会出现不定状态,具体见下图。 、
同步D触发器
一、电路组成
下图中左边为内部的电路组成,右边为逻辑表示:
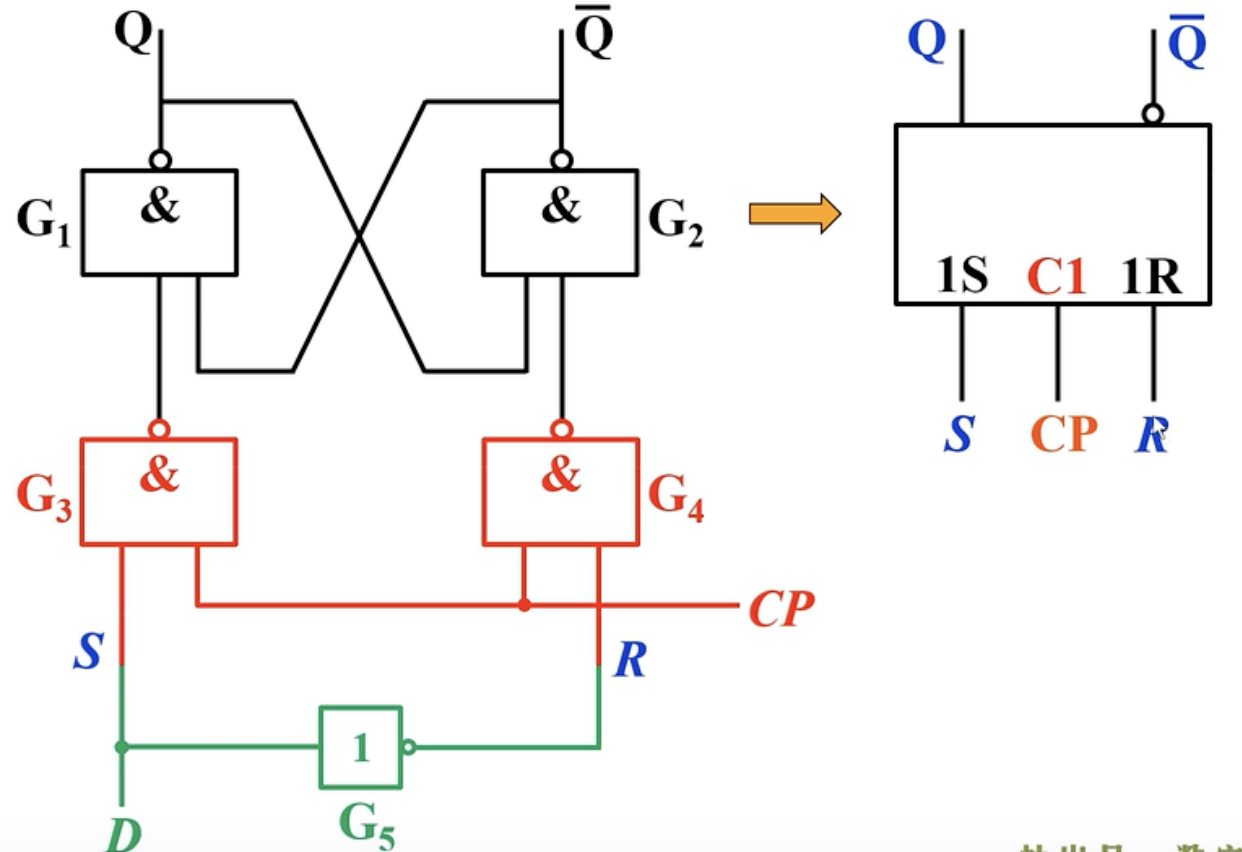
不难发现,同步D触发器就是把同步RS触发器 S和R用一个非门化简成了D,这样的好处就是完美地规避了约束条件的问题。
其他特性和同步RS触发器保持一致,都收到CP端的控制。
二、逻辑功能
功能也很简单,D端是1就置1,D端是0就置0。不存在输入有问题的情况,CP端置零也和原来一样起保持的作用。
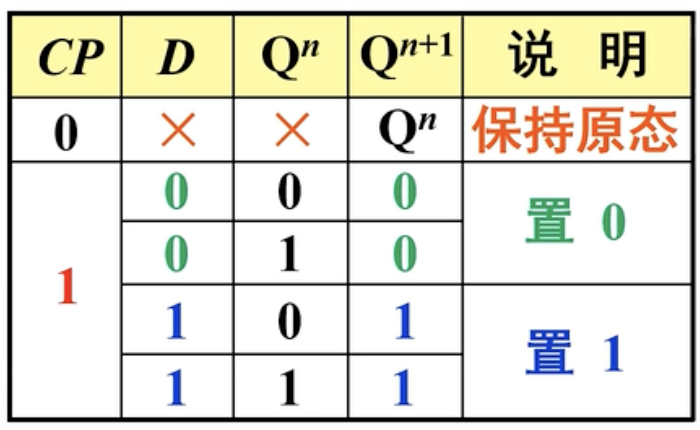
三、卡诺图与特性方程
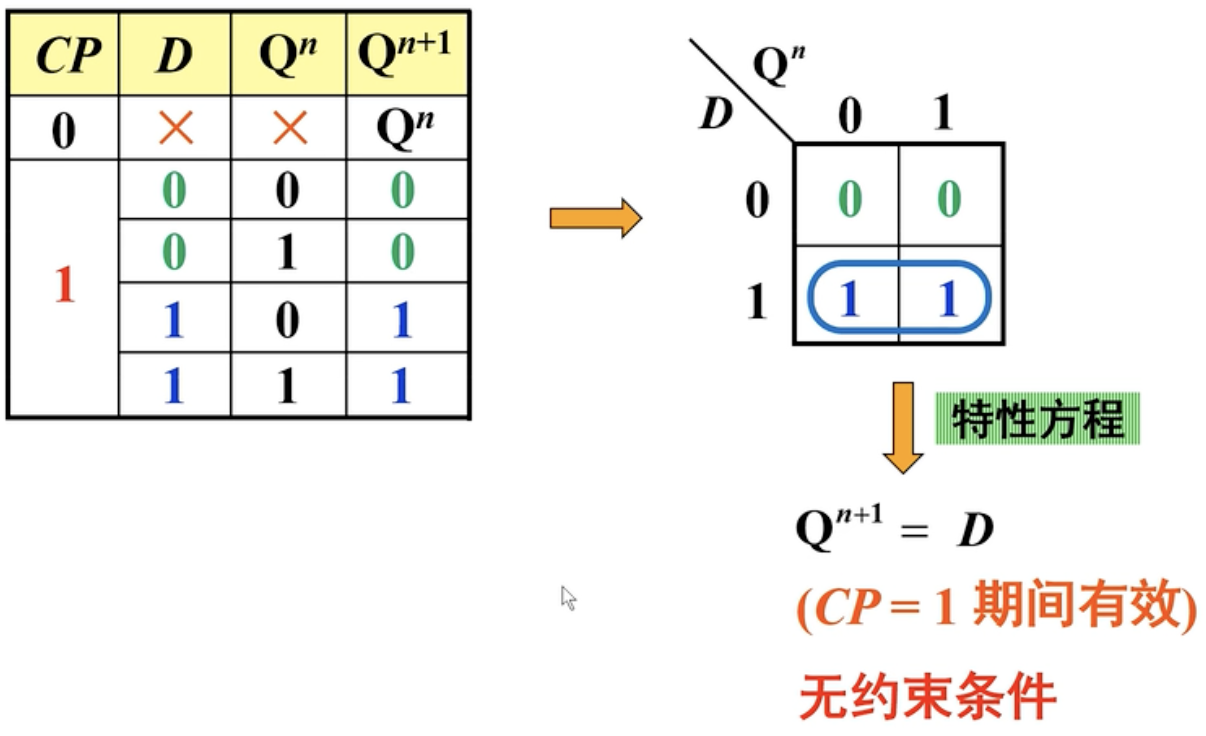
四、状态转移图
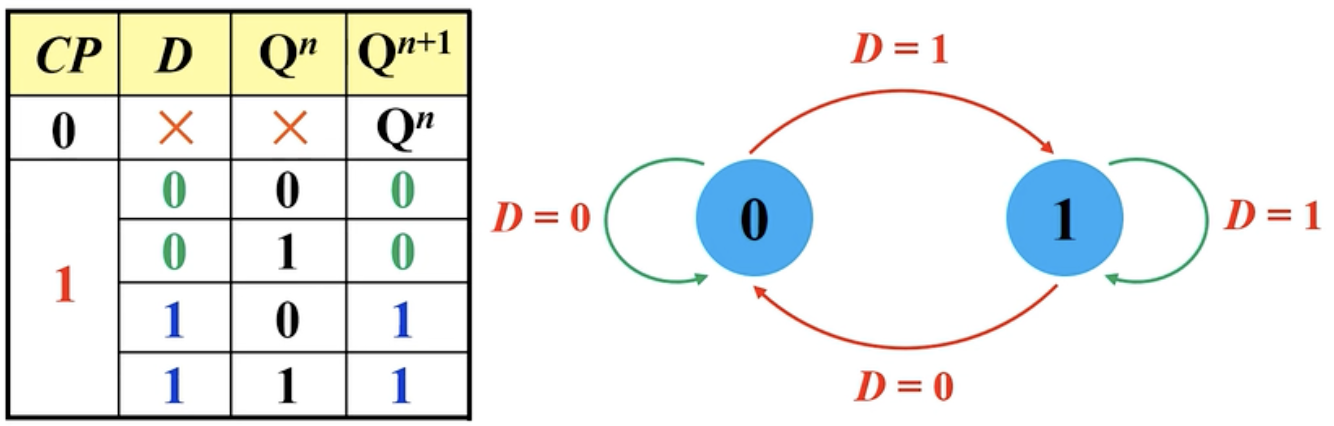
五、同步触发器的特点
- 优点:无需考虑约束条件的问题,优于同步RS触发器。
- 缺点:仍然存在空翻现象,限制了同步D触发器的应用。
六、集成同步D触发器:74LS375
这块芯片拥有13块管脚,可以理解为四个同步D触发器的拼接。
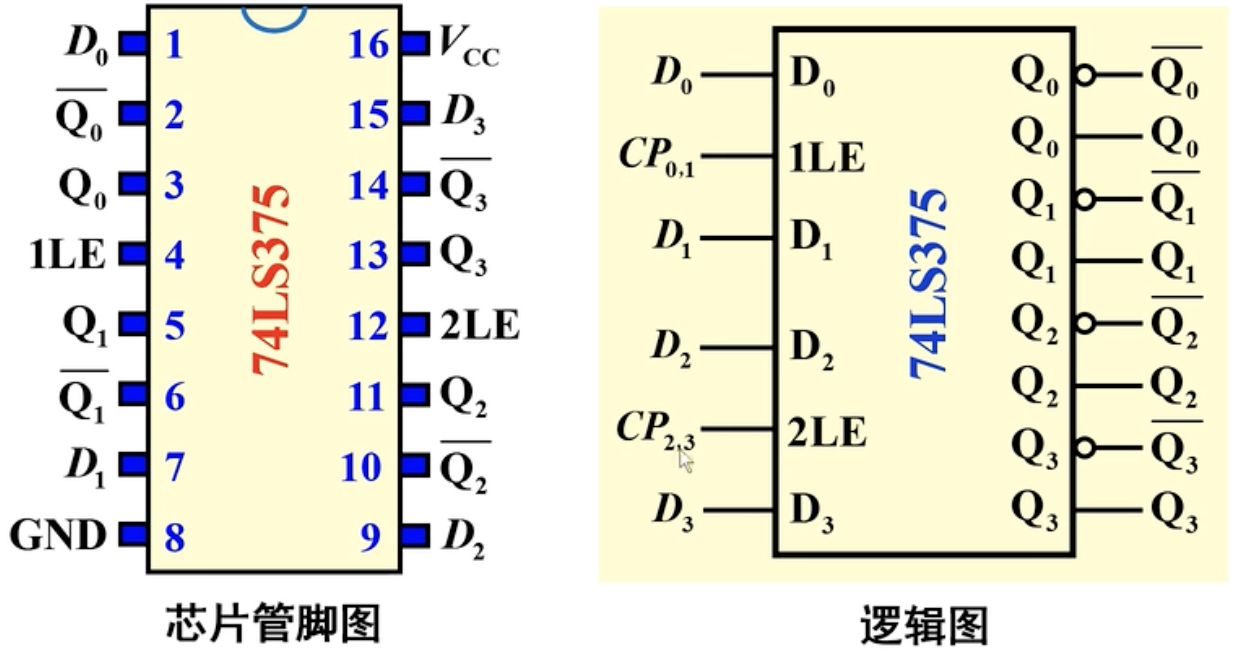
它的内部结构和上文提到的同步D触发器有所不同,区别在于上方的两个与非门被换成了或非门,下方的两个与非门被换成了与门,我们知道或非门的RS触发器的输入端左边是R右边是S,并且是高电平有效,所以D也在右边,为了和S端保持一致。
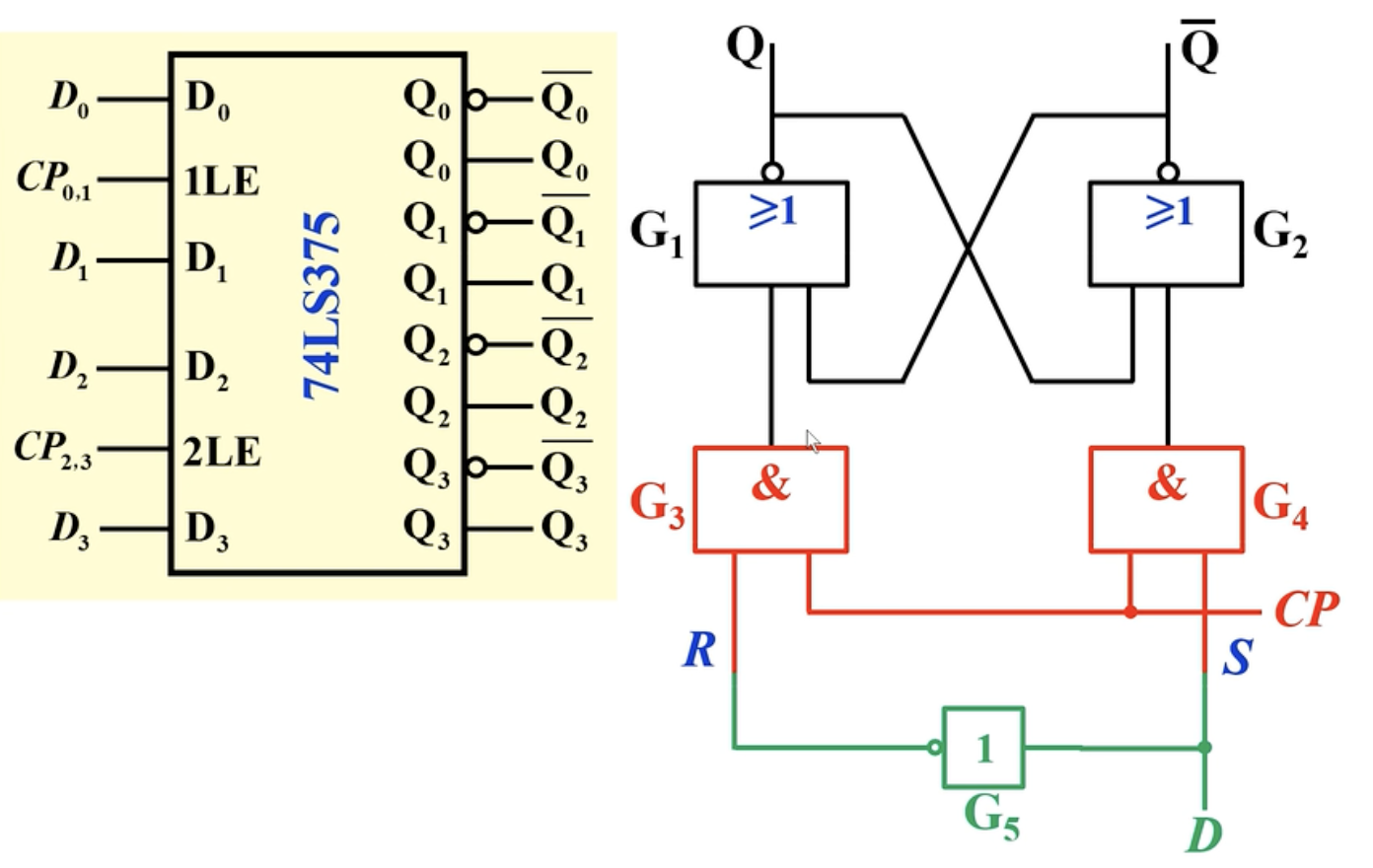
边沿D触发器
特性:只在时钟脉冲CP的上升沿或者下降沿接收输入信号,在其他的CP状态触发器不接受数据,并且保持原态。
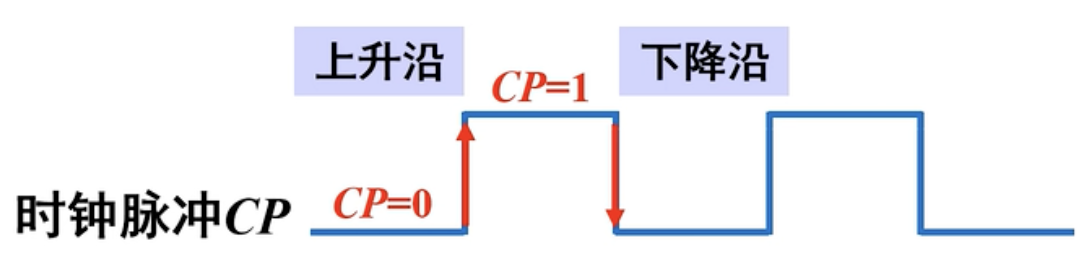
上升沿与下降沿:如下图中的两个红色箭头就分别表示上升沿和下降沿。
一、电路组成
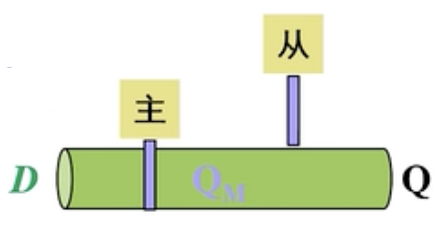
这是一个下降沿D触发器的电路组成图。
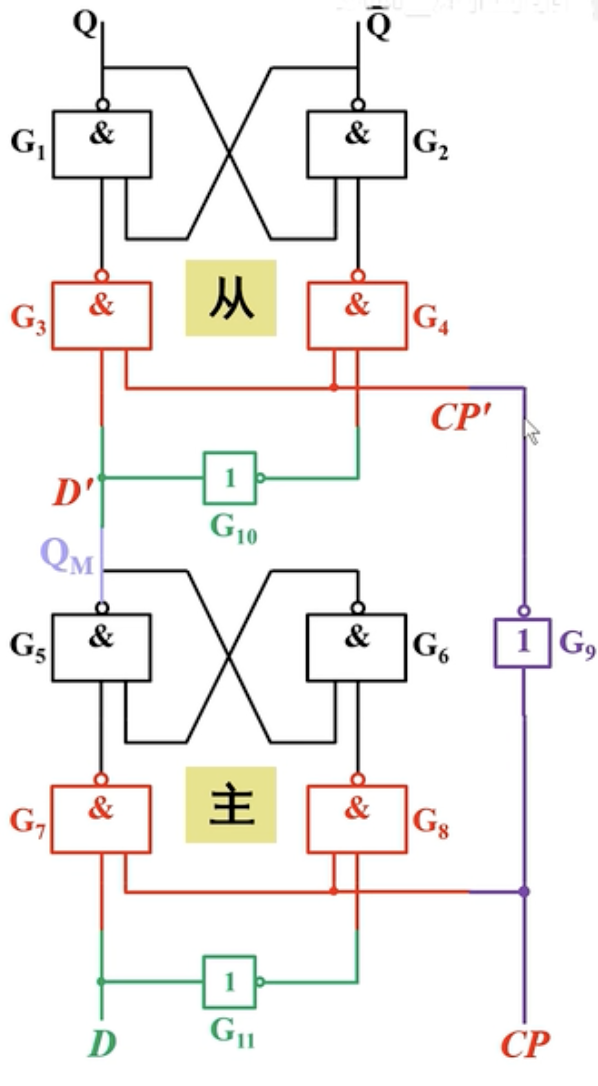
可以看出,边沿D触发器就是由两个同步D触发器上下拼接在一起,并且经过了一些特殊的改进而组成。不难分析出来,主从触发器是互斥的,主触发器工作,从触发器一定不工作;从触发器工作,主触发器也不会工作。
下降沿触发器的工作原理图:
在CP变化的时候,如果CP是从0->1,我们称为上升沿;如果CP是从1->0,我们称为下降沿。可以类比成下面这个水管图,上升沿CP变成了1,那么主触发器就工作了,左边的阀门打开。并且,这个时候从触发器不工作,所以右边的阀门关闭。这个时候就是保持。
但是如果CP从1->0,也就是下降沿。那么主阀门关闭,从阀门打开,这个时候
逻辑符号:
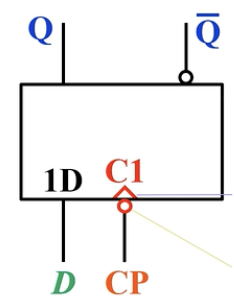
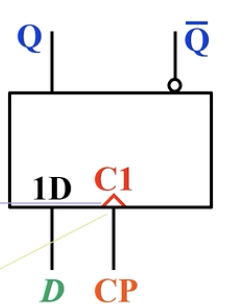
不难发现,其实他长得和同步D触发器一样,所以为了区分他们两个,给边沿D触发器的
二、特性方程、特性表
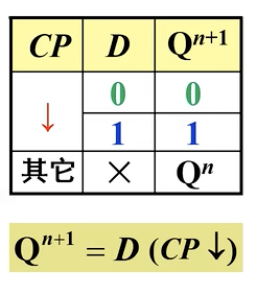
波形图分析:
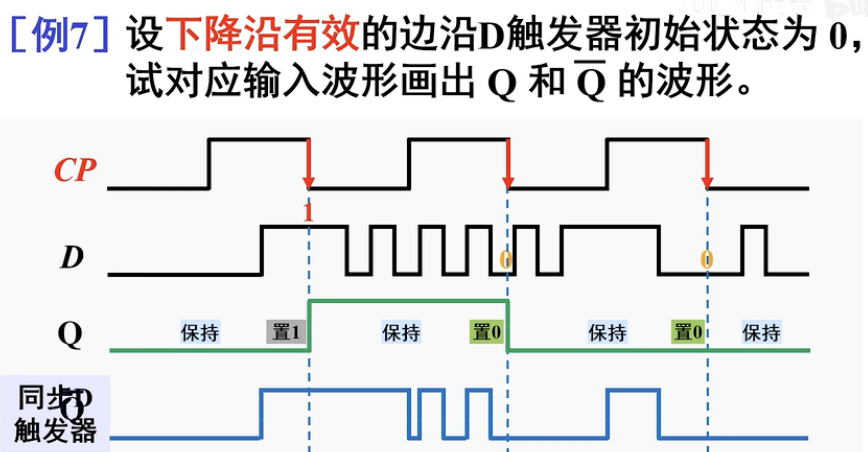
可以看出来,边沿触发器有一个区别于同步D触发器的很明显的特点:稳定,不容易“空翻”。
空翻现象就是指的是在CP没有变化的时候,
,输出跟随D改变的现象。因为对于边沿触发器来说,只要不是位于下降或者上升的边沿情况,都是保持的,也就不容易“空翻”了。
三、集成边沿D触发器:74LS74
对应的芯片管脚图和逻辑图:
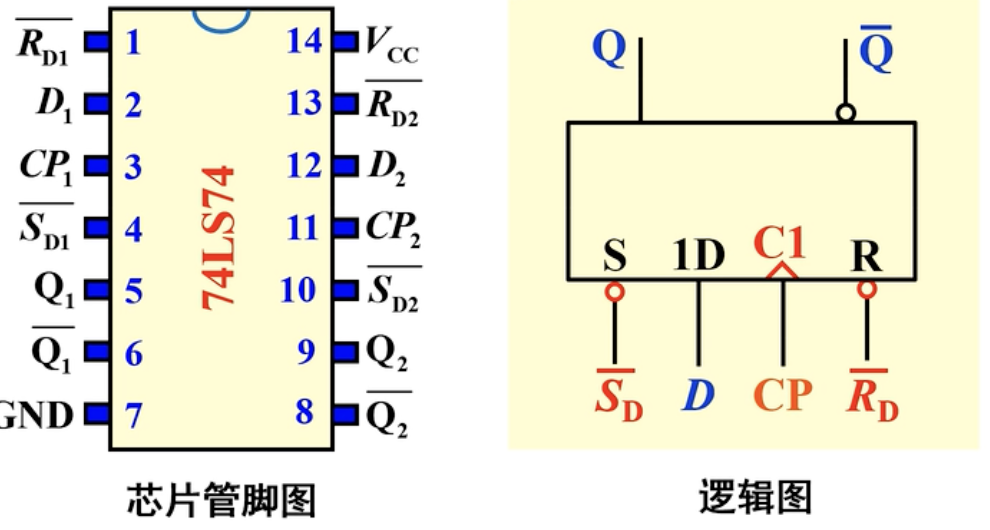
这里的
带有异步端边沿触发器的特性表:
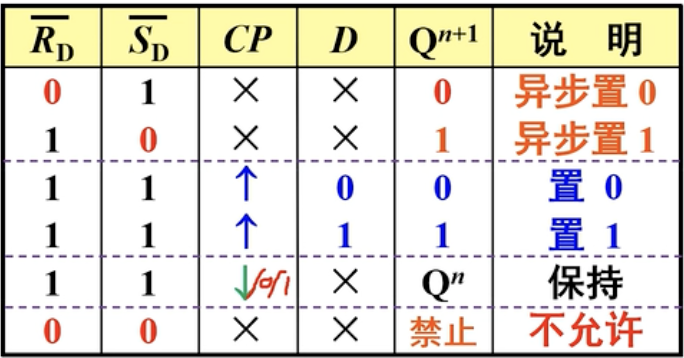
异步端优先级很高,一般起到预输入的作用,如果D和CP需要工作,一般需要将异步端置为零。但也可以利用它优先级高的特性,在工作中利用异步输入端强行置1或置0🤔。
带有异步输入端上升沿D触发器波形图分析:
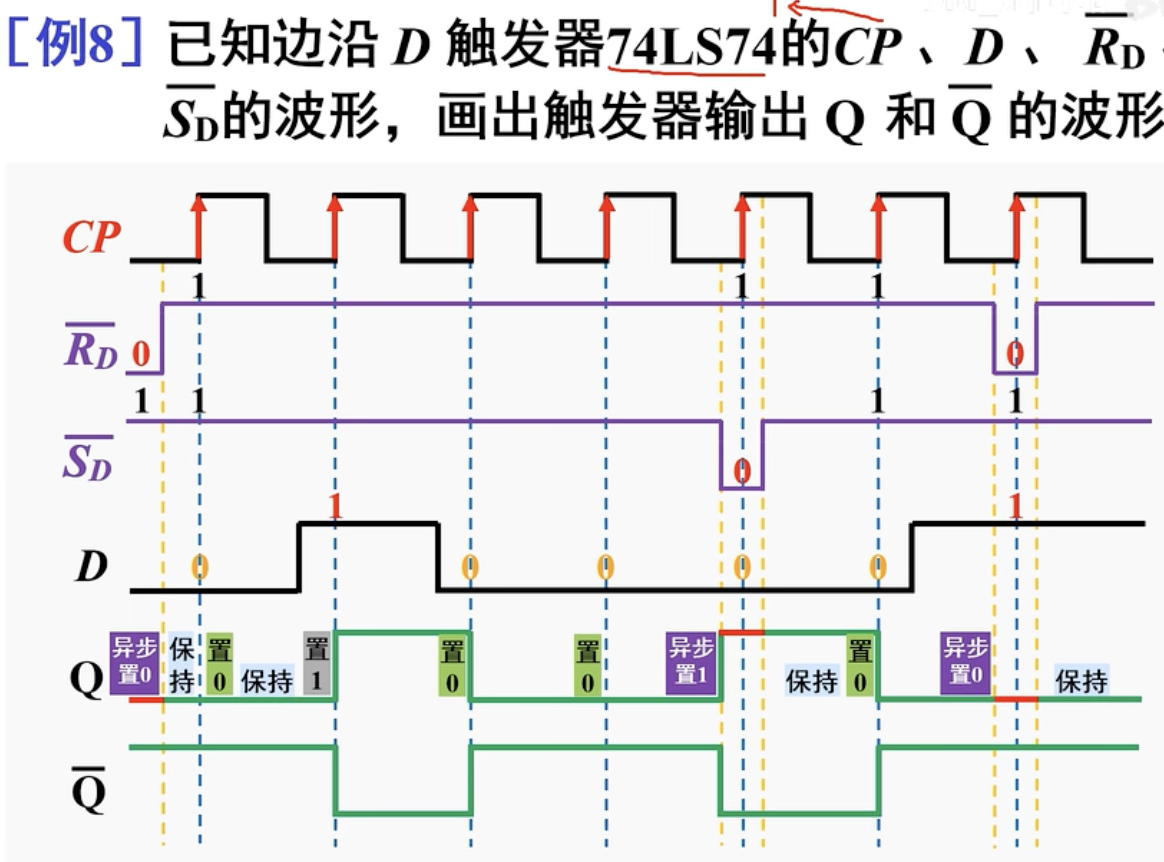
四、边沿D触发器的特点
优点:
- CP的上升沿或下降沿触发。
- 抗干扰能力强,解决了同步触发器的“空翻”现象。
缺点:
- 只有置1或置0功能,功能有限不方便。
边沿JK触发器
一、电路组成
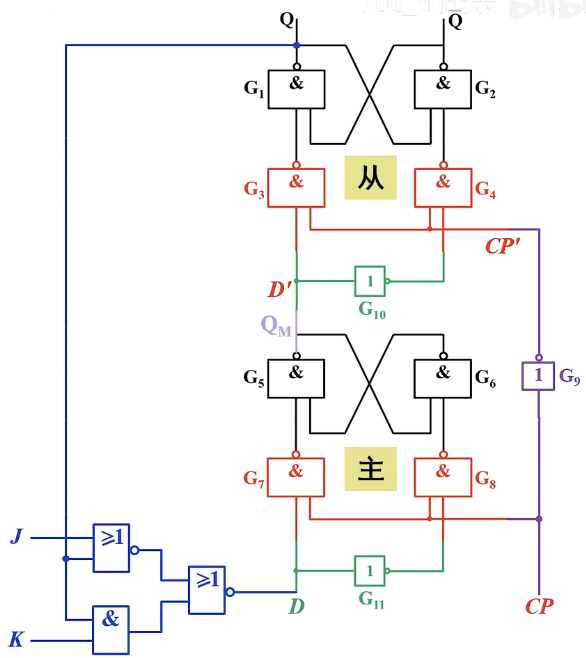
可以看出,边沿JK触发器是从边沿D触发器进行一些扩展得到的,右边这部分就是我们所学的边沿D触发器。
逻辑符号:
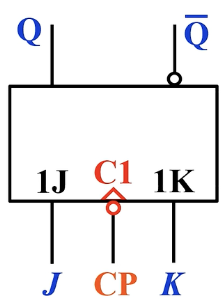
这里的三角形表示边沿,小⭕️代表下降沿触发;如果没有这个小三角形就变成了同步触发器。
二、工作原理
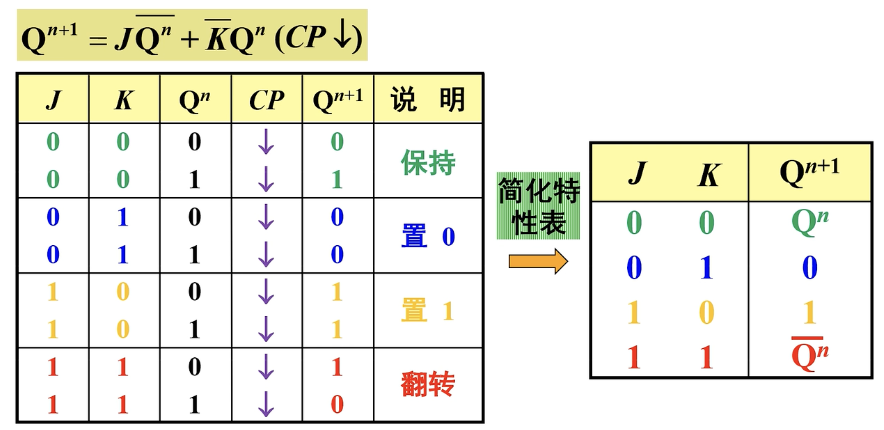
我们知道,右边这部分是边沿D触发器,它的特性方程是这样的:
我们加上左边新增的逻辑门电路,对他进行化简就能得到新的特性方程:

同样的可以得到它的特性表和简化特性表,通过这个特性表可以看出JK边沿触发器非常的强大,被称之为功能最齐全的一种触发器。拥有保持、置一、置零、翻转、防空翻功能。所以它也是使用最广泛的一种触发器。
波形图分析:
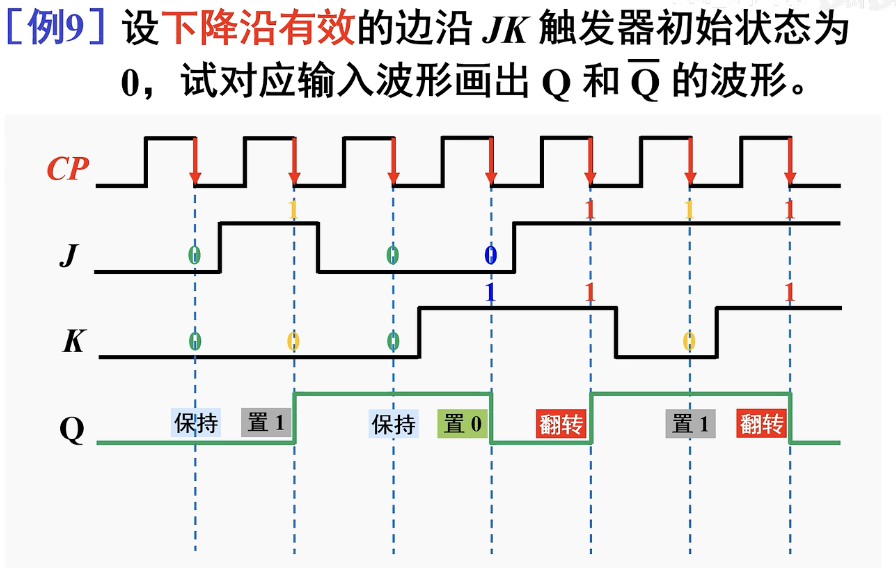
和 完全相反,这里没有写出来。
四、集成边沿JK触发器:74LS112
对应的芯片管脚图和逻辑图如下图所示:
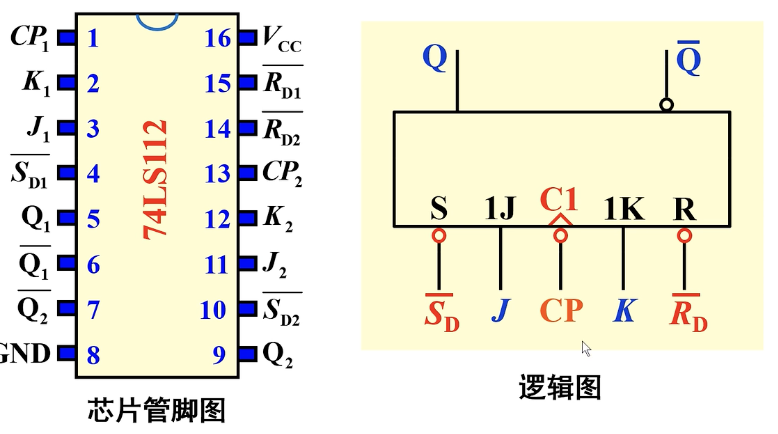
注意⚠️:这里的异步输入端是低电平0️⃣有效,触发器是下降⬇️沿触发的。
异步边沿JK触发器 74LS112对应的特性表如下图所示:
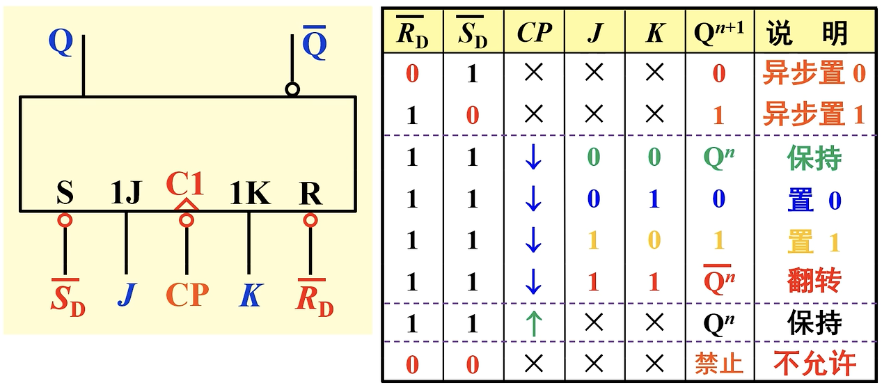
可以看出,和之前的边沿D触发器芯片一样,带有异步输入端后,异步输入端的优先级最高。并且在工作时,异步端置1️⃣,防止干扰JK触发器正常工作。同时,两个异步输入端不能同时为0️⃣,否则无效。
对应波形图的分析:
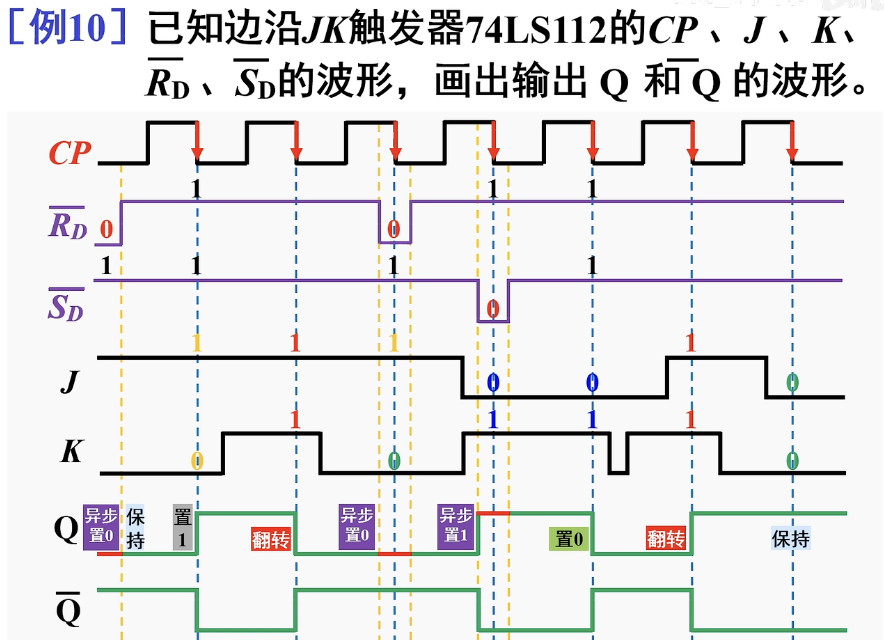
T触发器和T’触发器
T触发器和T’触发器都是由JK触发器或D触发器构成,主要用来简化集成计数器的逻辑电路。
一、T触发器
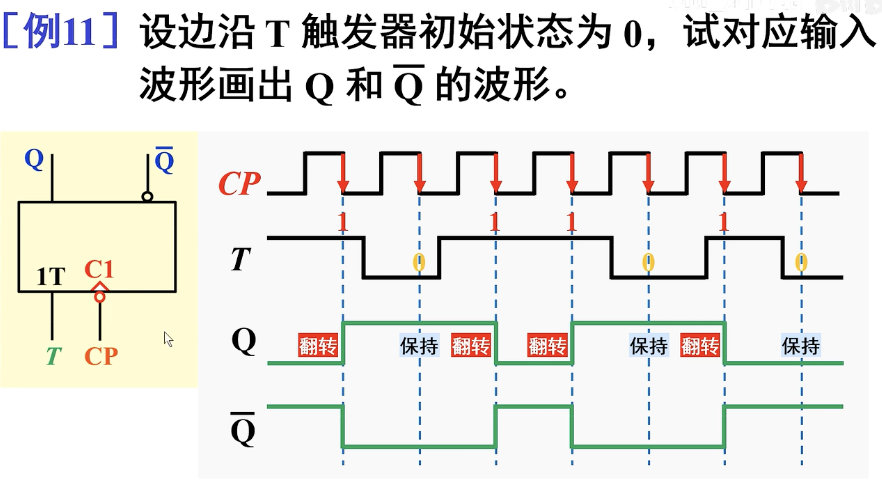
T触发器拥有翻转和保持两个功能。并且,又可以分为上升沿和下降沿两种T触发器。
逻辑符号:
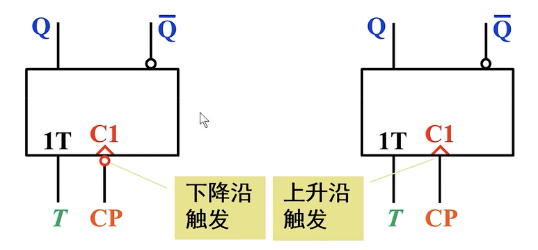
特性表:
T触发器的功能就是,在下降沿到来的时候,T为0就保持,T为1就翻转。
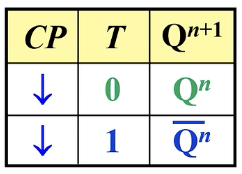
特性方程比较简单:
很容易看出来是异或。
用一个波形图进行分析:
二、T’触发器
T’触发器比T触发器还要简单,它的功能是在下降或者上升沿是进行一次翻转。
逻辑符号与特性表:
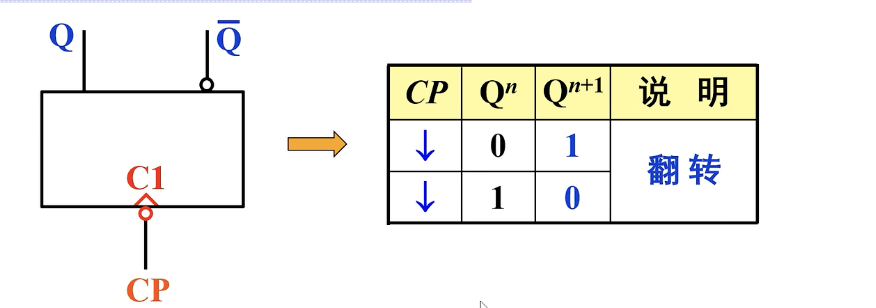
特性方程:
利用波形图进行分析:
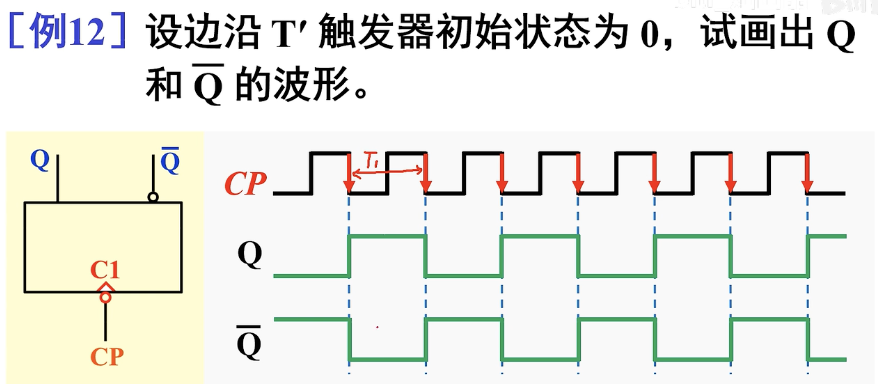
所以,T’触发器实际上就是一个“二分频器“,因为CP周期在T’的作用下变成Q被分成了远来的1/2。
主从JK触发器
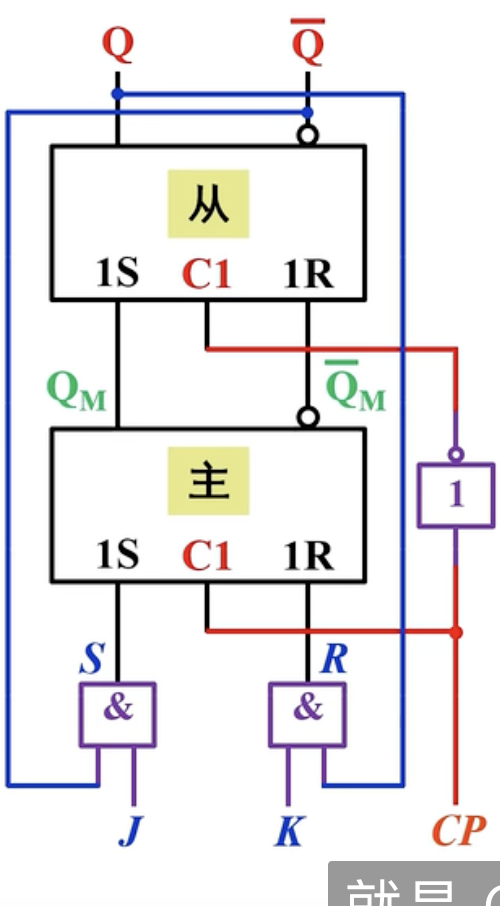
- J端:是由原来的Set变化而来
- K端:是由原来的Reset变化而来
JK触发器和RS触发器基本一样,唯一的不同是当J和K都置1时由原来的不允许变成了翻转。
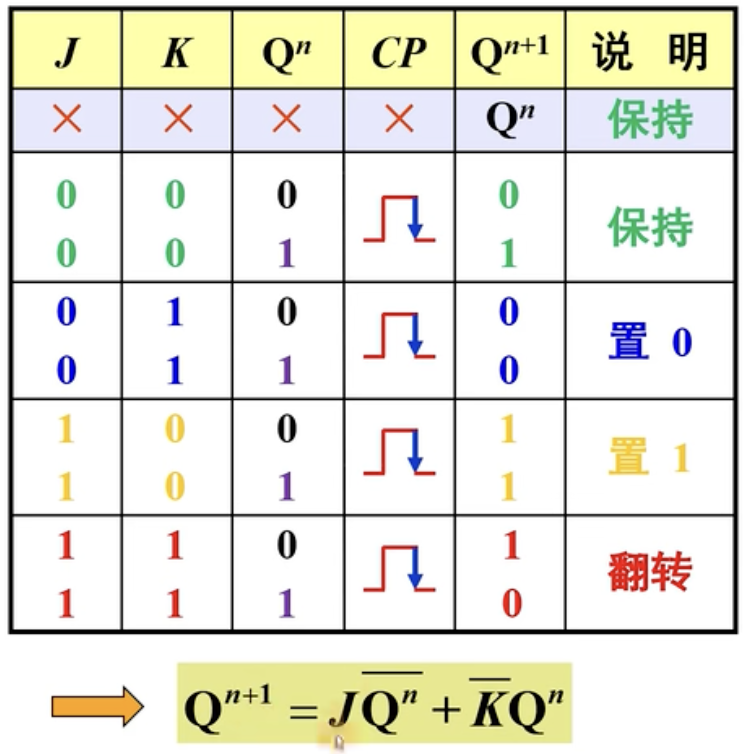
真值表与特性方程:
逻辑符号:
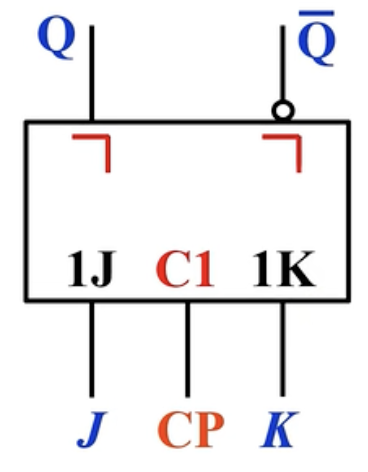
CP:正脉冲触发,表示在高电平接收信号,在下降沿时刻更新输出状态。
同步时序电路的设计
一、基本步骤
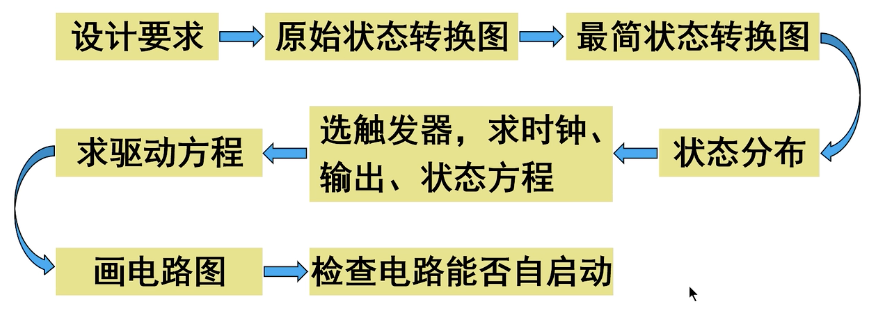
[例题-1]
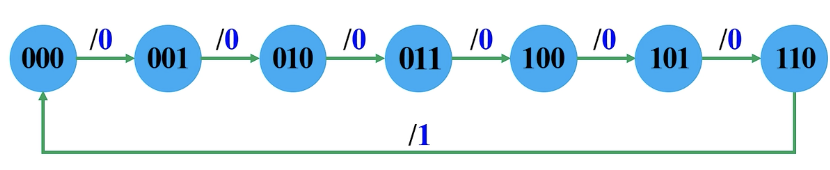
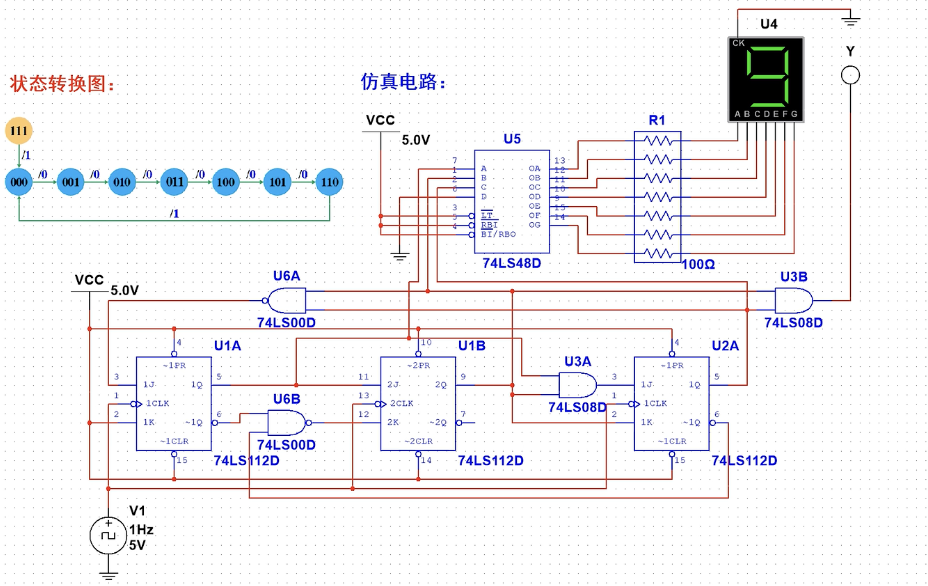
设计一个按自然态序变化的同步七进制加法计数器,计数规则为逢七进一,产生一个进位输出。
解:
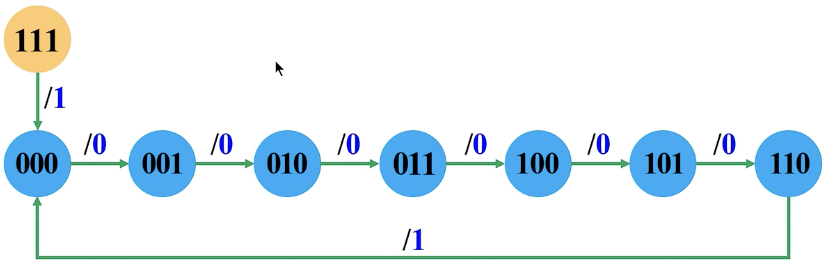
建立状态转化图

这里的
/0和/1为是否进位的表示,也就是进位的输出,只有逢七才进一位。所以在110的时候加一才会进位,这时候是/1。求方程
时钟方程:
输出方程:

状态方程:
先画出次态的卡诺图,再拆分开得各触发器的卡诺图。
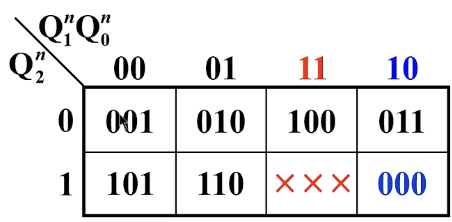
次态卡诺图:

拆开后各触发器的卡诺图:

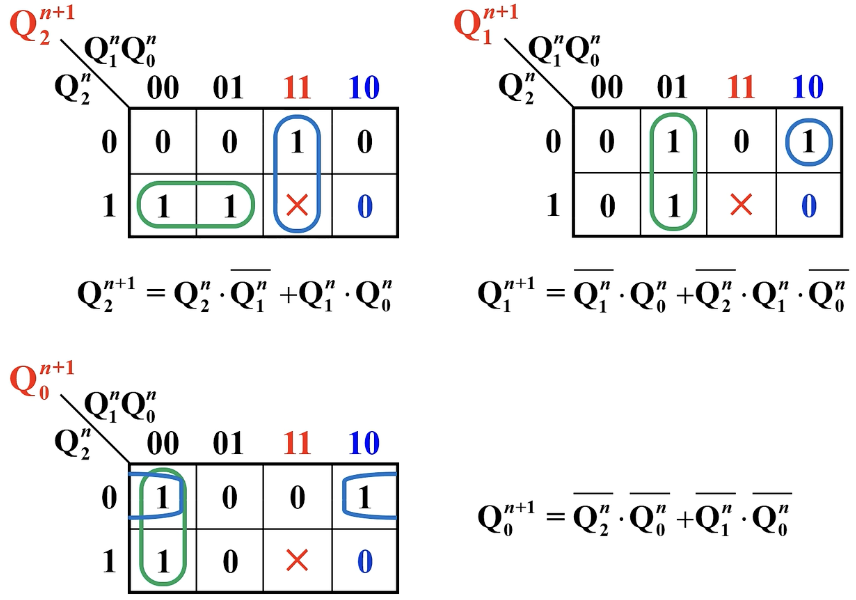
求驱动方程
变换状态方程,使之形式与选用触发器的特性方程一致,比较后得驱动方程。
比较并得到驱动方程:

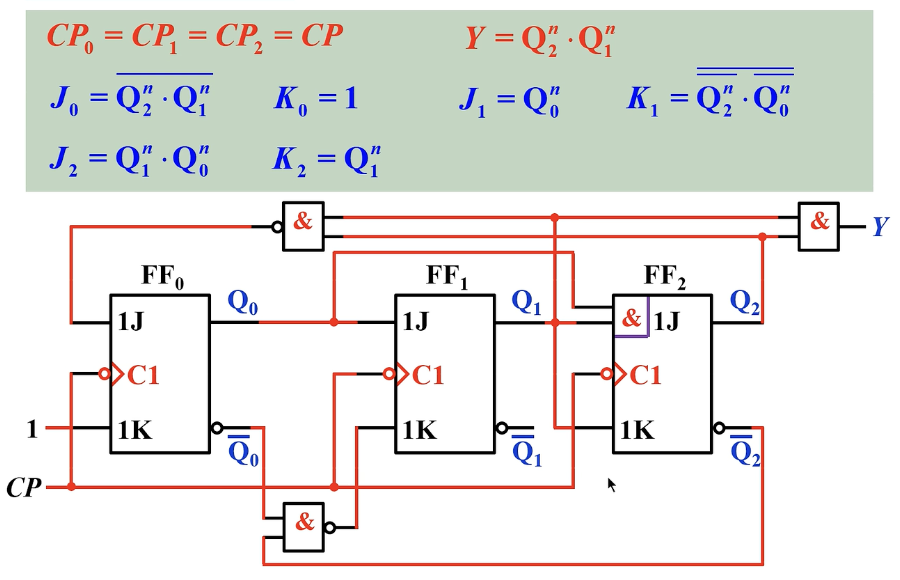
画电路图
结合驱动方程和输出方程画出电路图:

检查电路是否能自启动
能从无效的状态自己返回到正常状态称为自启动。
无效状态:
状态方程:

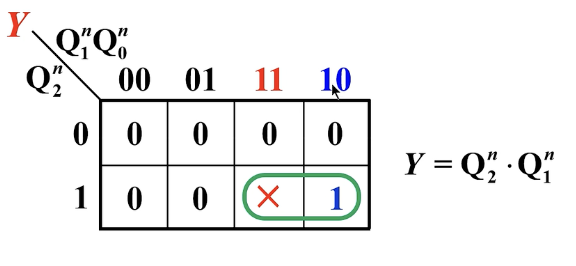
输出方程:
将无效状态带入到状态方程,得到次态为
000,并且输出是1,所以可以自启动。检验后得到对应的状态转换图:

Multism 仿真电路图:

- 标题: 数字逻辑电路笔记
- 作者: Shen Ying
- 创建于 : 2024-12-24 00:41:54
- 更新于 : 2025-01-02 16:47:01
- 链接: https://shenying.online/2024/12/24/数电笔记/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。